
【题目】已知函数f(x)![]() ,g(x)
,g(x)![]() 1.
1.
(1)若f(a)=2,求实数a的值;
(2)判断f(x)的单调性,并证明;
(3)设函数h(x)=g(x)![]() (x>0),若h(2t)+mh(t)+4>0对任意的正实数t恒成立,求实数m的取值范围.
(x>0),若h(2t)+mh(t)+4>0对任意的正实数t恒成立,求实数m的取值范围.
【答案】(1)a=log23;(2)函数f(x)在(﹣∞,0),(0,+∞)上单调递减,证明见解析(3)[﹣3,+∞).
【解析】
(1)根据f(a)=2,代入解析式求解.
(2)函数f(x)在(﹣∞,0),(0,+∞)上单调递减,用单调性的定义证明.
(3)化简得到![]() ,将
,将![]() 0对任意的正实数t恒成立,通过换元
0对任意的正实数t恒成立,通过换元![]() ,μ∈(2,+∞),转化为μ2+mμ+2>0对任意μ∈(2,+∞)恒成立,即
,μ∈(2,+∞),转化为μ2+mμ+2>0对任意μ∈(2,+∞)恒成立,即![]() 对任意μ∈(2,+∞)恒成立,再求解
对任意μ∈(2,+∞)恒成立,再求解![]() 最大值即可.
最大值即可.
(1)∵![]() ,
,
∴2a=3,
∴a=log23;
(2)函数f(x)在(﹣∞,0),(0,+∞)上单调递减,
证明如下:
函数的定义域为(﹣∞,0)∪(0,+∞),
因为f(-x)![]()
所以f(x)是奇函数
任取![]() 且
且![]()
![]() ,
,
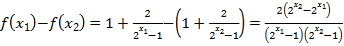
因为![]()
所以![]()
因为![]()
所以![]()
所以![]()
所以f(x)在(0,+∞)上单调递减,
又因为f(x)是奇函数
故函数f(x)在(﹣∞,0),(0,+∞)上单调递减;
(3)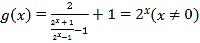 ,
,![]() ,
,
∴![]() 0对任意的正实数t恒成立,
0对任意的正实数t恒成立,
令![]() ,则μ∈(2,+∞),
,则μ∈(2,+∞),
∴μ2+mμ+2>0对任意μ∈(2,+∞)恒成立,
即![]() 对任意μ∈(2,+∞)恒成立,
对任意μ∈(2,+∞)恒成立,
又![]() 在(2,+∞)上单调递减,故
在(2,+∞)上单调递减,故![]() ,
,
则m≥﹣3,即实数m的取值范围为[﹣3,+∞).


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() ,其前
,其前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴若![]() ,
,![]() ,
,![]() (
(![]() ),求证:数列
),求证:数列![]() 是等比数列;
是等比数列;
⑵若数列![]() 是等比数列,求
是等比数列,求![]() ,
,![]() 的值;
的值;
⑶若![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有一家大型共享汽车公司,在市场上分别投放了黄、蓝两种颜色的汽车,已知黄、蓝两种颜色的汽车的投放比例为![]() .监管部门为了了解这两种颜色汽车的质量,决定从投放到市场上的汽车中随机抽取5辆汽车进行试驾体验,假设每辆汽车被抽取的时能性相同.
.监管部门为了了解这两种颜色汽车的质量,决定从投放到市场上的汽车中随机抽取5辆汽车进行试驾体验,假设每辆汽车被抽取的时能性相同.
(1)求抽取的5辆汽车中恰有2辆是蓝色汽车的概率;
(2)在试驾体验过程中,发现蓝色汽车存在一定质量问题,监管部门决定从投放的汽车中随机地抽取一辆送技术部门作进一步抽样检测,并规定:若抽取的是黄色汽车.则将其放回市场,并继续随机地抽取下一辆汽车;若抽到的是蓝色汽车,则抽样结束;并规定抽样的次数不超过![]() 次,在抽样结束时,若已取到的黄色汽车数以
次,在抽样结束时,若已取到的黄色汽车数以![]() 表示,求
表示,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=(3m2﹣2m)x![]() 在(0,+∞)上单调递增,g(x)=x2﹣4x+t.
在(0,+∞)上单调递增,g(x)=x2﹣4x+t.
(1)求实数m的值;
(2)当x∈[1,9]时,记f(x),g(x)的值域分别为集合A,B,设命题p:x∈A,命题q:x∈B,若命题q是命题p的必要不充分条件,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A.命题“若x2﹣3x+2=0,则x=2”的逆否命题为“若x≠2,则x2﹣3x+2≠0”
B.“a=2”是“函数f(x)=ax在区间(﹣∞,+∞)上为增函数”的充分不必要条件
C.命题“x∈R,使得x2+x+1<0”的否定是:“x∈R,均有x2+x+1≥0”
D.“若f ′(![]() )=0,则
)=0,则![]() 为y=f(x)的极值点”为真命题
为y=f(x)的极值点”为真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com