
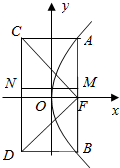
 如图,已知抛物线方程y2=2px(p>0),AB是过焦点F的一条弦,点A(x1,y1),B(x2,y2).求证:
如图,已知抛物线方程y2=2px(p>0),AB是过焦点F的一条弦,点A(x1,y1),B(x2,y2).求证:分析 (1)设直线AB的方程为x=my+$\frac{p}{2}$,代入y2=2px,再利用韦达定理,即可得到结论;
(2)利用抛物线的定义,可得|AB|=x1+x2+p;结合y1y2=-p2,进一步得到|AB|=x1+x2+p=$\frac{2p}{si{n}^{2}θ}$.
解答 证明:(1)设直线AB的方程为x=my+$\frac{p}{2}$,代入y2=2px,可得y2-2pmy-p2=0,
∴y1y2=-p2,∴x1x2=$\frac{({y}_{1}{y}_{2})^{2}}{4{p}^{2}}=\frac{{p}^{4}}{4{p}^{2}}=\frac{{p}^{2}}{4}$;
(2)∵AB是过抛物线y2=2px(p>0)的焦点的弦,
∴由抛物线定义可得|AB|=x1+$\frac{p}{2}$+x2+$\frac{p}{2}$=x1+x2+p;
由(1)知,y1y2=-p2,y1+y2=2pm,
∴${{y}_{1}}^{2}+{{y}_{2}}^{2}$=(y1+y2)2-2y1y2=4p2m2+2p2,
又${{y}_{1}}^{2}+{{y}_{2}}^{2}$=2p(x1+x2)=4p2m2+2p2,∴x1+x2=2pm2+p,
∴θ=90°时,m=0,∴|AB|=2p=$\frac{2p}{si{n}^{2}θ}$;θ≠90°时,m=$\frac{1}{tanθ}$,|AB|=$\frac{2p}{ta{n}^{2}θ}$+2p=$\frac{2p}{si{n}^{2}θ}$.
∴|AB|=x1+x2+p=$\frac{2p}{si{n}^{2}θ}$.
点评 本题考查直线与抛物线的位置关系,考查韦达定理的运用,考查弦长的计算,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | a>0且b2-4ac>0 | B. | -$\frac{b}{2a}$>0 | C. | b2-4ac>0 | D. | -$\frac{b}{2a}<0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com