
【题目】已知函数 ![]() ,
,
(1)若 ![]() ,求
,求 ![]() 在区间
在区间 ![]() 上的最小值;
上的最小值;
(2)若 ![]() 在区间
在区间 ![]() 上有最大值
上有最大值 ![]() ,求实数
,求实数 ![]() 的值
的值
【答案】
(1)解:若 ![]() ,则
,则 ![]()
函数图像开口向下,对称轴为 ![]() ,所以函数
,所以函数 ![]() 在区间
在区间 ![]() 上是单调递增的,在区间
上是单调递增的,在区间 ![]() 上是单调递减的,有又
上是单调递减的,有又 ![]() ,
, ![]()
![]()
(2)解:对称轴为 ![]()
当 ![]() 时,函数在
时,函数在 ![]() 在区间
在区间 ![]() 上是单调递减的,则
上是单调递减的,则![]() ,即
,即 ![]() ;
;
当 ![]() 时,函数
时,函数 ![]() 在区间
在区间 ![]() 上是单调递增的,在区间
上是单调递增的,在区间 ![]() 上是单调递减的,则
上是单调递减的,则 ![]() ,解得
,解得 ![]() ,不符合;
,不符合;
当 ![]() 时,函数
时,函数 ![]() 在区间
在区间 ![]() 上是单调递增的,则
上是单调递增的,则![]() ,解得
,解得 ![]()
综上所述, ![]() 或
或 ![]()
【解析】本题主要考查函数的最值问题。(1)求函数在闭区间的最值问题,主要要研究函数的单调性,本题主要根据二次函数的图像,判断单调性进而求出最值。(2)根据最值求参数,因为函数的对称轴不确定,所以要对对称轴进行讨论,结合函数图像,化静为动的思想来求解。
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数![]() 的图象是一条抛物线,对称轴方程为
的图象是一条抛物线,对称轴方程为![]() 顶点坐标是
顶点坐标是![]() ;当
;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣ ![]() (k+1)x2+3kx+1,其中k∈R.
(k+1)x2+3kx+1,其中k∈R.
(1)当k=3时,求函数f(x)在[0,5]上的值域;
(2)若函数f(x)在[1,2]上的最小值为3,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的函数 ![]() 是偶函数,且满足
是偶函数,且满足 ![]() 上的解析式为
上的解析式为 ![]() ,过点
,过点 ![]() 作斜率为k的直线l , 若直线l与函数
作斜率为k的直线l , 若直线l与函数 ![]() 的图象至少有4个公共点,则实数k的取值范围是
的图象至少有4个公共点,则实数k的取值范围是
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将三角形ADE沿AE折起,则下列说法正确的是________(填序号).
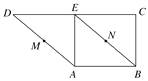
①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置,都有MN⊥AE;③不论D折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com