
【题目】已知函数f(x)=lnx![]() (b∈R),g(x)
(b∈R),g(x)![]() .
.
(1)讨论函数f(x)的单调性
(2)是否存在实数b使得函数y=f(x)在x∈(![]() ,+∞)上的图象存在函数y=g(x)的图象上方的点?若存在,请求出最小整数b的值,若不存在,请说明理由.(参考数据ln2=0.6931,
,+∞)上的图象存在函数y=g(x)的图象上方的点?若存在,请求出最小整数b的值,若不存在,请说明理由.(参考数据ln2=0.6931,![]() 1.6487)
1.6487)
【答案】(1)答案不唯一,具体见解析(2)存在,最小b的整数值为2
【解析】
(1)求出函数的导数,分类讨论![]() 可得函数
可得函数![]() 的单调性;
的单调性;
(2)假设存在实数![]() 使得函数
使得函数![]() 在
在![]() 上的图象有在函数
上的图象有在函数![]() 的图象上方的点,则使不等式
的图象上方的点,则使不等式![]() 成立,即
成立,即![]() 成立,令
成立,令![]() ,求新函数的最值即可判断.
,求新函数的最值即可判断.
(1)函数f(x)的定义域为(0,+∞),且f′(x)![]() ,
,
当b≤0时、f′(x)>0,函数f(x)在(0,+∞)上单调递增,
当b>0时,若0<x<b,则f′(x)<0,若x>b,则f′(x)>0,
函数f(x)在(0,b)上单调递减,在(b,+∞)上单调递增,
综上得:当b≤0时,函数f(x)在(0,+∞)上单调递增;
当b>0时,函数f(x)在(0,b)上单调递减,在(b,+∞)上单调递增;
(2)假设存在实数b满足题意,则存在x∈(![]() ,+∞)
,+∞)
使不等式lnx![]() 成立,
成立,
即b>ex﹣xlnx成立,
令h(x)=ex﹣xlnx,则h′(x)=ex﹣lnx﹣1,
令φ(x)=ex﹣lnx﹣1,则φ′(x)=ex![]() ,
,
因为φ′(x)在(![]() ,+∞)上单调递增、且φ′(
,+∞)上单调递增、且φ′(![]() )
)![]() 2<0,φ′(1)=e﹣1>0,
2<0,φ′(1)=e﹣1>0,
且φ'(x)的图象在(![]() ,1)上连续,
,1)上连续,
所以存在x0∈(![]() ,1)使φ′(x0)=0.即
,1)使φ′(x0)=0.即![]() 0,即x0=﹣lnx0,
0,即x0=﹣lnx0,
当x∈(![]() ,x0)时,φ(x)单调递减,当x∈(x0,+∞)时,φ(x)单调递增,
,x0)时,φ(x)单调递减,当x∈(x0,+∞)时,φ(x)单调递增,
则φ(x)的最小值φ(x0)![]() lnx0﹣1=x0
lnx0﹣1=x0![]() 1≥2
1≥2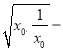 1=1>0,
1=1>0,
所以h'(x)>0,h(x)在区间(![]() ,+∞)内单调递增,
,+∞)内单调递增,
所以h(x)>h(![]() )
)![]() ln
ln![]() ln2=1.9952
ln2=1.9952
所以存在实数b满足题意,且最小b的整数值为2.


科目:高中数学 来源: 题型:
【题目】如图所示1,已知四边形ABCD满足![]() ,
,![]() ,E是BC的中点.将
,E是BC的中点.将![]() 沿着AE翻折成
沿着AE翻折成![]() ,使平面
,使平面![]() 平面AECD,F为CD的中点,如图所示2.
平面AECD,F为CD的中点,如图所示2.
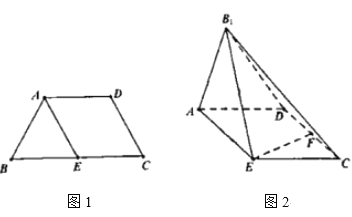
(1)求证:![]() 平面
平面![]() ;
;
(2)求AE到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,延长
两点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 的周长为8.
的周长为8.

(1)求![]() 的离心率及方程;
的离心率及方程;
(2)试问:是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线![]() 是焦点在
是焦点在![]() 轴上的椭圆,两个焦点分别是是
轴上的椭圆,两个焦点分别是是![]() ,
,![]() ,且
,且![]() ,
,![]() 是曲线上的任意一点,且点
是曲线上的任意一点,且点![]() 到两个焦点距离之和为4.
到两个焦点距离之和为4.
(1)求![]() 的标准方程;
的标准方程;
(2)设![]() 的左顶点为
的左顶点为![]() ,若直线
,若直线![]() :
:![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() (
(![]() ,
,![]() 不是左右顶点),且满足
不是左右顶点),且满足![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标点xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsinθ=6.
(1)A为曲线C1上的动点,点M在线段OA上,且满足|OM||OA|=36,求点M的轨迹C2的直角坐标方程;
(2)点E的极坐标为(4,![]() ),点F在曲线C2上,求△OEF面积的最大值
),点F在曲线C2上,求△OEF面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若在两个成语中,一个成语的末字恰是另一成语的首字,则称这两个成语有顶真关系,现从分别贴有成语“人定胜天”、“争先恐后”、“一马当先”、“天马行空”、“先发制人”的5张大小形状完全相同卡片中,任意抽取2张,则这2张卡片上的成语有顶真关系的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)若数列![]() 是等差数列,且
是等差数列,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)若数列![]() 满足
满足![]()
![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
(3)设数列![]() 是等比数列,试探究当正实数
是等比数列,试探究当正实数![]() 满足什么条件时,数列
满足什么条件时,数列![]() 具有如下性质
具有如下性质![]() :对于任意的
:对于任意的![]()
![]() ,都存在
,都存在![]() 使得
使得![]() ,写出你的探求过程,并求出满足条件的正实数
,写出你的探求过程,并求出满足条件的正实数![]() 的集合.
的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年5月20日以来,广东自西北到东南出现了一次明显降雨.为了对某地的降雨情况进行统计,气象部门对当地20日~28日9天记录了其中100小时的降雨情况,得到每小时降雨情况的频率分布直方图如下:

若根据往年防汛经验,每小时降雨量在![]() 时,要保持二级警戒,每小时降雨量在
时,要保持二级警戒,每小时降雨量在![]() 时,要保持一级警戒.
时,要保持一级警戒.
(1)若从记录的这100小时中按照警戒级别采用分层抽样的方法抽取10小时进行深度分析.
①求一级警戒和二级警戒各抽取多少小时;
②若从这10个小时中任选2个小时,则这2个小时中恰好有1小时属于一级警戒的概率.(2)若以每组的中点代表该组数据值,求这100小时内的平均降雨量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是![]() ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.
(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com