
【题目】已知直线l1经过两点(-1,-2)、(-1,4),直线l2经过两点(2,1)、(x,6),且l1||l2 , 则x=( ).
A.2
B.-2
C.4
D.1
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为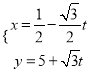 (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系.
轴的正半轴为极轴建立坐标系.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)射线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是( )
A.(x-2)2+(y-1)2=1
B.(x-2)2+(y-3)2=1
C.(x-3)2+(y-2)2=1
D.(x-3)2+(y-1)2=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查者100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图,若日销量不低于50件,则称当日为“畅销日”.
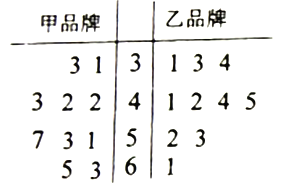
(1)现从甲品牌日销量大于40且小于60的样本中任取两天,求这两天都是“畅销日”的概率;
(2)用抽取的样本估计这100天的销售情况,请完成这两种品牌100天销量的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为品牌与“畅销日”天数有关.
的把握认为品牌与“畅销日”天数有关.
附: 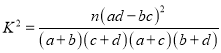 (其中
(其中![]() )
)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
畅销日天数 | 非畅销日天数 | 合计 | |
甲品牌 | |||
乙品牌 | |||
合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2003年至2015年北京市电影放映场次(单位:万次)的情况如图所示,下列函数模型中,最不适合近似描述这13年间电影放映场次逐年变化规律的是( )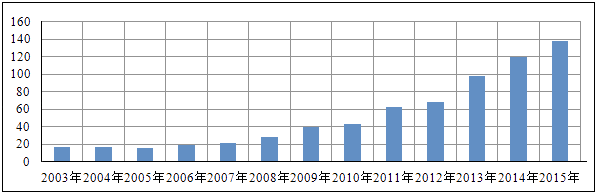
A.f(x)=ax2+bx+c
B.f(x)=aex+b
C.f(x)=eax+b
D.f(x)=alnx+b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com