
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 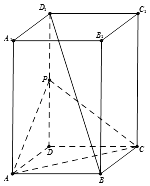
(1)求证:直线BD1∥平面PAC
(2)求证:平面PAC⊥平面BDD1B1 .
【答案】
(1)证明:连接BD交AC于O点,连接OP,
因为O为矩形对角线的交点,O为BD的中点,P为DD1的中点,
则OP∥BD1,又因为OP面APC,BD1面APC
所以直线BD1∥平面PAC
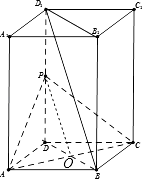
(2)证明:因为AB=AD=1,所以矩形ABCD为正方形,所以AC⊥BD,
由长方体可知,DD1⊥AC,而BD∩DD1=D,
所以AC⊥面BDD1B1,且AC面PAC,
则平面PAC⊥平面BDD1B1
【解析】(1)连接BD交AC于O点,连接OP,运用三角形的中位线定理和线面平行的判定定理,即可得证;(2)由线面垂直的判定定理,证得AC⊥面BDD1B1 , 再由面面垂直的判定定理即可得证.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证: 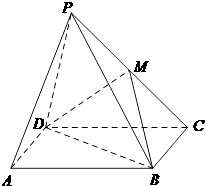
(1)PA∥平面MDB;
(2)PD⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (其中常数a>0,且a≠1).
(其中常数a>0,且a≠1).
(1)当a=10时,解关于x的方程f(x)=m(其中常数m>2 ![]() );
);
(2)若函数f(x)在(﹣∞,2]上的最小值是一个与a无关的常数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场种植黄瓜,根据多年的市场行情得知,从春节起的300天内,黄瓜市场售价与上市时间的关系用图1所示的一条折线表示,黄瓜的种植成本与上市时间的关系用图2所示的抛物线表示.(注:市场售价和种植成本的单位:元/kg,时间单位:天)
(1)写出图1表示的市场售价与时间的函数关系式P=f(t);写出图2表示的种植成本与时间的函数关系式Q=g(x);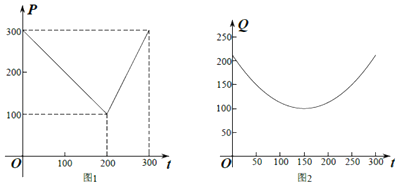
(2)认定市场售价减去种植成本为纯收益,问从春节开始的第几天上市的黄瓜纯收益最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={y|y=x2﹣2x﹣3,x∈R},B={x|log2x<﹣1},C={k|函数f(x)= ![]() 在(0,+∞)上是增函数}.
在(0,+∞)上是增函数}.
(1)求A,B,C;
(2)求A∩C,(UB)∪C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+a2﹣1.
(1)若对任意的x∈R均有f(1﹣x)=f(1+x),求实数a的值;
(2)当x∈[﹣1,1]时,求f(x)的最小值,用g(a)表示其最小值,判断g(a)的奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)(x>0)满足:f(xy)=f(x)+f(y),当x<1时f(x)>0,且f( ![]() )=1;
)=1;
(1)证明:y=f(x)是(x>0)上的减函数;
(2)解不等式f(x﹣3)>f( ![]() )﹣2.
)﹣2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com