
(本题15分)已知点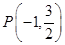 是椭圆E:
是椭圆E: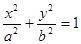 (
(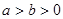 )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设A、B是椭圆E上两个动点,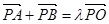 (
(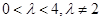 ).求证:直线AB的斜率为定值;
).求证:直线AB的斜率为定值;
(Ⅲ)在(Ⅱ)的条件下,当△PAB面积取得最大值时,求λ的值.
(1) 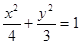 (2)根据已知的向量的坐标关系,结合点差法来得到直线的斜率。
(2)根据已知的向量的坐标关系,结合点差法来得到直线的斜率。
(3) 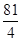
【解析】
试题分析:解:(Ⅰ)∵PF1⊥x轴,
∴F1(-1,0),c=1,F2(1,0),
|PF2|= ,2a=|PF1|+|PF2|=4,a=2,b2=3,
,2a=|PF1|+|PF2|=4,a=2,b2=3,
椭圆E的方程为: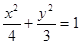 ;…………………4分
;…………………4分
(Ⅱ)设A(x1,y1)、B(x2,y2),由 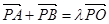 得
得
(x1+1,y1-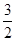 )+(x2+1,y2-
)+(x2+1,y2-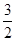 )=
)= (1,-
(1,- 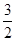 ),
),
所以x1+x2= -2
-2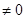 ,y1+y2=
,y1+y2=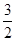 (2-
(2- )
)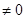 ………①
………①
又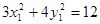 ,
,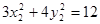 ,
,
两式相减得3(x1+x2)(x1-x2)+ 4(y1+y2)(y1-y2)=0………..②
以①式代入可得AB的斜率k=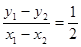 为定值; ……………9分
为定值; ……………9分
(Ⅲ)设直线AB的方程为y=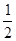 x+t,
x+t,
与 联立消去y并整理得
x2+tx+t2-3=0, △=3(4-t2),
联立消去y并整理得
x2+tx+t2-3=0, △=3(4-t2),
AB|= ,
,
点P到直线AB的距离为d= ,
,
△PAB的面积为S=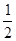 |AB|×d=
|AB|×d= , ………10分
, ………10分
设f(t)=S2=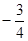 (t4-4t3+16t-16)
(-2<t<2),
(t4-4t3+16t-16)
(-2<t<2),
f’(t)=-3(t3-3t2+4)=-3(t+1)(t-2)2,由f’(t)=0及-2<t<2得t=-1.
当t∈(-2,-1)时,f’(t)>0,当t∈(-1,2)时,f’(t)<0,f(t)=-1时取得最大值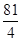 ,
,
所以S的最大值为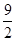 .此时x1+x2=-t=1=
.此时x1+x2=-t=1= -2,
-2, =3. ………………15分
=3. ………………15分
考点:椭圆的方程,向量
点评:解析几何中的圆锥曲线的求解,一般运用待定系数法来求解,同时运用设而不求的思想来研究直线与椭圆的位置关系,属于中档题。


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
(本题15分)已知椭圆![]() 的离心率为
的离心率为![]() ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为![]() ,直线
,直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() ,
,![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若![]() ,且
,且![]() ,求
,求![]() 的值(
的值(![]() 点为坐标
点为坐标![]() 原点);
原点);
(Ⅲ)若坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三上学期期中考试理科数学试卷(解析版) 题型:解答题
. (本题满分15分)已知点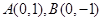 ,
,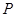 为一个动点,且直线
为一个动点,且直线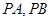 的斜率之积为
的斜率之积为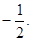
(I)求动点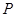 的轨迹
的轨迹 的方程;
的方程;
(II)设 ,过点
,过点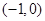 的直线
的直线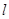 交
交 于
于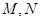 两点,
两点, 的面积记为S,若对满足条件的任意直线
的面积记为S,若对满足条件的任意直线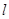 ,不等式
,不等式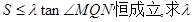 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三第一学期期末考试文科数学 题型:解答题
(本题15分)已知曲线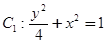 与曲线
与曲线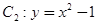 ,设点
,设点 是曲线
是曲线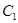 上任意一点,直线
上任意一点,直线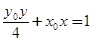 与曲线
与曲线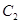 交于
交于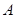 、
、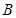 两点.
两点.
(1)判断直线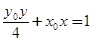 与曲线
与曲线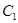 的位置关系;
的位置关系;
(2)以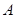 、
、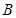 两点为切点分别作曲线
两点为切点分别作曲线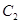 的切线,设两切线的交点为
的切线,设两切线的交点为 ,求证:点
,求证:点 到直线
到直线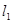 :
: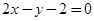 与
与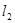 :
: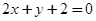 距离的乘积为定值.
距离的乘积为定值.
查看答案和解析>>
科目:高中数学 来源:2010年浙江省高一下学期期中考试数学(8-13班) 题型:解答题
(本题满分15分)已知点(1,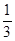 )是函数
)是函数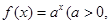 且
且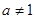 )的图象上一点,等比数列
)的图象上一点,等比数列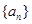 的前n项和为
的前n项和为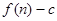 ,数列
,数列
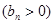 的首项为c,且前n项和
的首项为c,且前n项和 满足
满足
 -
-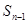 =
=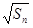 +
+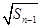 (n
(n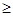 2).
2).
(Ⅰ)求数列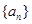 和
和 的通项公式;
的通项公式;
(Ⅱ)若数列{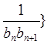 前n项和为
前n项和为 ,问
,问 >
> 的最小正整数n是多少?
的最小正整数n是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com