
| רҵ�Կ� | רҵ���Կ� | �ϼ� | |
| �� | 30 | 10 | 40 |
| Ů | 35 | 5 | 40 |
| �ϼ� | 65 | 15 | 80 |
| P��K�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.306 | 3.841 | 5.021 | 6.635 |
���� ��1������k2���㹫ʽ���ɵó���
��2����ͼ��֪��80λ��ҵ�����µĹ������ѧ��ѧרҵ�Կڵ�Ƶ�ʣ�
��3��������֪X����B��4��$\frac{13}{16}$�������ɵó�E��X����
��� �⣺��1���������k2=$\frac{80��30��5-35��10��^{2}}{40��40��65��15}$=$\frac{80}{39}$��3.841��
�ʲ����ڷ�����ĸ��ʲ�����5%��ǰ���£���Ϊ����ҵ�����µĹ������ѧ��ѧרҵ�Կ����Ա��йء���
��2����ͼ��֪��80λ��ҵ�����µĹ������ѧ��ѧרҵ�Կڵ�Ƶ��p=$\frac{65}{80}$=$\frac{13}{16}$��
��3��������֪X����B��4��$\frac{13}{16}$������E��X��=np=4��$\frac{13}{16}$=$\frac{13}{4}$��
���� ���⿼���˶����Լ���ԭ��������ֲ��м�����ѧ������������������������������������е��⣮


 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{2}$ | B�� | �� | C�� | 2�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x��=x${\;}^{\frac{1}{3}}$ | B�� | f��x��=sinx | C�� | f��x��=cosx | D�� | f��x��=log2��x2+1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
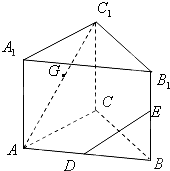 ��ͼ������������ABC-A1B1C1�У�D��E��G�ֱ���AB��BB1��AC1���е㣬AB=BB1=2��
��ͼ������������ABC-A1B1C1�У�D��E��G�ֱ���AB��BB1��AC1���е㣬AB=BB1=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{2}$ | B�� | 4 | C�� | $\frac{5}{2}$ | D�� | $\frac{7}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 120 | B�� | 720 | C�� | 1440 | D�� | 5040 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
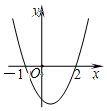
| A�� | x��-1 | B�� | x��2 | C�� | -1��x��2 | D�� | x��-1��x��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��0��\frac{1}{2}���ȣ�2��+�ޣ�$ | B�� | $��\frac{1}{2}��1���ȣ�2��+�ޣ�$ | C�� | ��2��+�ޣ� | D�� | $��\frac{1}{2}��1��$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com