
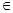 (0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
(0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由. 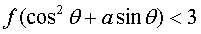 对任意的θ∈(0,π)恒成立.
对任意的θ∈(0,π)恒成立.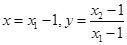 代入条件③,整理变形后借助于条件②可证出结论.
代入条件③,整理变形后借助于条件②可证出结论.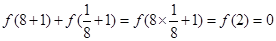 ,可得
,可得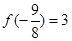 ,根据条件②判断函数的单调性,根据已知条件把f(cos2θ+asinθ)<3化为cos2θ+asinθ<
,根据条件②判断函数的单调性,根据已知条件把f(cos2θ+asinθ)<3化为cos2θ+asinθ< 或1<cos2θ+asinθ<9,对任意的θ∈(0,π)恒成立,换元和分离参数即可求得a的范围..
或1<cos2θ+asinθ<9,对任意的θ∈(0,π)恒成立,换元和分离参数即可求得a的范围..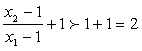 从而
从而 ,
,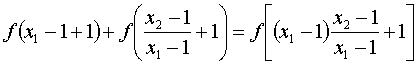
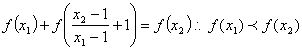
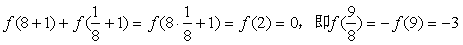 因为f(x)为奇函数,所以
因为f(x)为奇函数,所以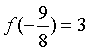 ,于是f(x)<3的解集为;
,于是f(x)<3的解集为;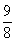 )∪(1,9),于是问题转化为是否存在实数a,使
)∪(1,9),于是问题转化为是否存在实数a,使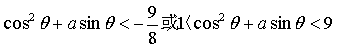 对任意的θ∈(0,π)恒成立,令sinθ=t,则t∈(0,1]于是
对任意的θ∈(0,π)恒成立,令sinθ=t,则t∈(0,1]于是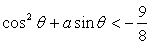 恒成立等价于
恒成立等价于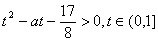 恒成立.即
恒成立.即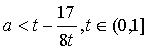 恒成立,当t→0时,
恒成立,当t→0时,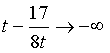 ,故不存在实数a使
,故不存在实数a使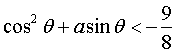 对任意的
对任意的 恒成立,得a>1,
恒成立,得a>1,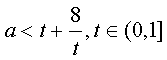 ,
,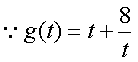 在(0,1]单调递减,于是g(t)min=9,故a<9 于是存在a∈(1,9)使1<cos2θ+asinθ<9 对任意的θ∈(0,π)恒成立.
在(0,1]单调递减,于是g(t)min=9,故a<9 于是存在a∈(1,9)使1<cos2θ+asinθ<9 对任意的θ∈(0,π)恒成立.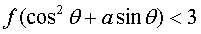 对任意的θ∈(0,π)恒成立.……………………(14分).
对任意的θ∈(0,π)恒成立.……………………(14分).

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源:不详 题型:单选题
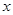 ,符号
,符号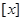 表示不超过
表示不超过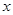 的最大整数,例如
的最大整数,例如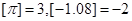 ,定义函数
,定义函数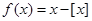 ,则下列命题中正确的是( )
,则下列命题中正确的是( )A.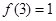 | B.方程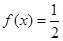 有且仅有一个解 有且仅有一个解 |
C.函数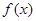 是周期函数 是周期函数 | D.函数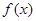 是增函数 是增函数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
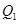 和日产量
和日产量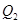 均为价格
均为价格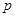 的函数,且
的函数,且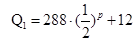
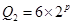 ,日成本C关于日产量
,日成本C关于日产量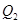 的关系为
的关系为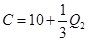
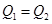 时的价格为均衡价格,求均衡价格
时的价格为均衡价格,求均衡价格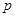 ;
;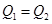 时日利润
时日利润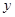 最大,求
最大,求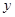
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
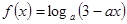
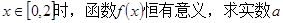 的取值范围;
的取值范围;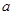 ,使得函数
,使得函数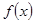 在区间
在区间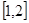 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出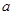 值;若不存在,说明理由。
值;若不存在,说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
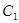 的方程是
的方程是
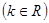 ,曲线
,曲线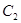 的方程是
的方程是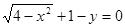 ,给出下列结论:
,给出下列结论: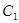 恒过定点
恒过定点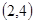 ;
;  ②曲线
②曲线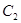 的图形是一个圆;
的图形是一个圆;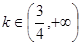 时,
时,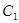 与
与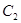 有一个公共点; ④若
有一个公共点; ④若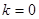 时,则
时,则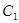 与
与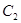 必无公共点。
必无公共点。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com