
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | 2-$\sqrt{2}$ |
分析 由题意可得$\overrightarrow{c}$($\overrightarrow{a}$+$\overrightarrow{b}$)≥1,只需求|$\overrightarrow{a}$+$\overrightarrow{b}$-2$\overrightarrow{c}$|2最大值即可,然后根据数量积的运算法则展开即可求得.
解答 解:∵$\overrightarrow{a}$•$\overrightarrow{b}$=0,($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)≤0,
∴$\overrightarrow{a}•\overrightarrow{b}$-$\overrightarrow{a}•\overrightarrow{c}$-$\overrightarrow{b}$•$\overrightarrow{c}$+${\overrightarrow{c}}^{2}$≤0,
∴$\overrightarrow{c}$($\overrightarrow{a}$+$\overrightarrow{b}$)≥1,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$-2$\overrightarrow{c}$|2=($\overrightarrow{a}$-$\overrightarrow{c}$)2+($\overrightarrow{b}$-$\overrightarrow{c}$)2+2($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=4-2$\overrightarrow{c}$($\overrightarrow{a}$+$\overrightarrow{b}$)+2[-($\overrightarrow{c}$($\overrightarrow{a}$+$\overrightarrow{b}$)+1]=6-4$\overrightarrow{c}$($\overrightarrow{a}$+$\overrightarrow{b}$)≤6-4=2,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$-2$\overrightarrow{c}$|的最大值$\sqrt{2}$
故选:B
点评 本题考查平面向量数量积的运算和模的计算问题,考查学生灵活应用知识分析、解决问题的能力,属中档题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:选择题
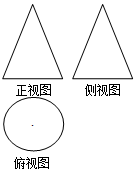 如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )| A. | $\frac{{2\sqrt{2}}}{3}π$ | B. | $2\sqrt{2}π$ | C. | $8\sqrt{2}π$ | D. | $\frac{{8\sqrt{2}}}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在频率分布直方图中,众数左边和右边的直方图的面积相等 | |
| B. | 为调查高三年级的240名学生完成作业所需的时间,由教务处对高三年级的学生进行编号,从001到240抽取学号最后一位为3的学生进行调查,则这种抽样方法为分层抽样 | |
| C. | “x≠1”是“x2-3x+2≠0”的充分不必要条件 | |
| D. | 命题p:“?x0∈R,${x_0}^2-3{x_0}+2<0$”的否定为:“?x∈R,x2-3x+2≥0” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com