
【题目】如图,ABCD是块矩形硬纸板,其中AB=2AD,AD=![]() ,E为DC的中点,将它沿AE折成直二面角D-AE-B.
,E为DC的中点,将它沿AE折成直二面角D-AE-B.
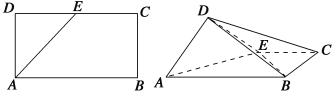
(1)求证:AD⊥平面BDE;
(2)求二面角B-AD-E的余弦值.
【答案】(1)见解析(2)![]()
【解析】
试题分析:(1)本题为折叠问题,注意折叠过程中得不变性.证线面垂直可回到判定定理(化为线与两条相交直线垂直来证).另也可建立空间坐标系,运用向量运算来解决.
(2)由(1)已经建立空间坐标系,则关键是算出两个平面的法向量,利用法向量的数量积,可算出二面角的余弦.(注意观察二面角为钝角还是锐角对应余弦的负和正).
试题解析: (1)由题设可知AD⊥DE,取AE中点O,连接OD,BE.∵AD=DE=![]() ,∴OD⊥AE.又二面角D-AE-B为直二面角,∴OD⊥平面ABCE.又AE=BE=2,AB=2
,∴OD⊥AE.又二面角D-AE-B为直二面角,∴OD⊥平面ABCE.又AE=BE=2,AB=2![]() ,∴AB2=AE2+BE2.∴AE⊥BE.取AB中点F,连接OF,则OF∥EB.∴OF⊥AE.以点O为原点,OA,OF,OD分别为x,y,z轴建立空间直角坐标系(如图),
,∴AB2=AE2+BE2.∴AE⊥BE.取AB中点F,连接OF,则OF∥EB.∴OF⊥AE.以点O为原点,OA,OF,OD分别为x,y,z轴建立空间直角坐标系(如图),
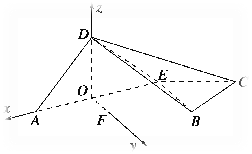
则A(1,0,0),D(0,0,1),B(-1,2,0),E(-1,0,0),![]() =(-1,0,1),
=(-1,0,1),![]() =(1,-2,1),
=(1,-2,1),![]() =(0,2,0),
=(0,2,0),
设n=(x1,y1,z1)是平面BDE的法向量,
则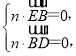 即
即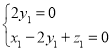 取x1=1,则z1=-1.
取x1=1,则z1=-1.
于是n=(1,0,-1).∴n=-![]() .∴n∥
.∴n∥![]() .∴AD⊥平面BDE.
.∴AD⊥平面BDE.
(2)设m=(x2,y2,z2)是平面ABD的一个法向量,
则m·![]() =0,m·
=0,m·![]() =0,∴
=0,∴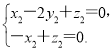 取x2=1,则y2=1,z2=1,则m=(1,1,1),平面ADE的法向量
取x2=1,则y2=1,z2=1,则m=(1,1,1),平面ADE的法向量![]() =(0,1,0).∴cos〈m,
=(0,1,0).∴cos〈m,![]() 〉=
〉=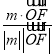 =
=![]() =
=![]() .
.
∴二面角B-AD-E的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,
,![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=![]() x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(﹣
x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(﹣![]() ,
, ![]() ).
).
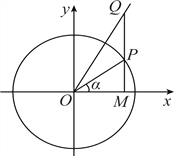
(Ⅰ)若sinα=![]() ,求cos∠POQ;
,求cos∠POQ;
(Ⅱ)求△OPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国魏人刘徽,自撰《海岛算经》,专论测高望远。其中有一题:今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从后表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高及去表各几何? 译文如下:要测量海岛上一座山峰![]() 的高度
的高度![]() ,立两根高均为
,立两根高均为![]() 丈的标杆
丈的标杆![]() 和
和![]() ,前后标杆相距
,前后标杆相距![]() 步,使后标杆杆脚
步,使后标杆杆脚![]() 与前标杆杆脚
与前标杆杆脚![]() 与山峰脚
与山峰脚![]() 在同一直线上,从前标杆杆脚
在同一直线上,从前标杆杆脚![]() 退行
退行![]() 步到
步到![]() ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,![]() 、
、![]() 、
、![]() 三点共线,从后标杆杆脚
三点共线,从后标杆杆脚![]() 退行
退行![]() 步到
步到![]() ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,![]() 、
、![]() 、
、![]() 三点也共线,问岛峰的高度
三点也共线,问岛峰的高度![]() 步. (古制:
步. (古制:![]() 步=
步=![]() 尺,
尺,![]() 里=
里=![]() 丈=
丈=![]() 尺=
尺=![]() 步)
步)
查看答案和解析>>
科目:高中数学 来源: 题型:
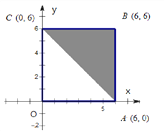
【题目】如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界)。
(Ⅰ)向区域A随机抛掷一粒黄豆,求黄豆落在区域B的概率;
(Ⅱ)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)落在区域B的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com