Question

如图，四棱锥P—ABCD中，PD⊥平面ABCD，PA与平面ABCD所成的角为60°，在四边形ABCD中，∠D=∠DAB=90°，AB=4，CD=1,AD=2.

(1)建立适当的坐标系，并写出点B、P的坐标；

(2)求异面直线PA与BC所成的角；

(3)若PB的中点为M，求证：平面AMC⊥平面PBC.

Answer 1

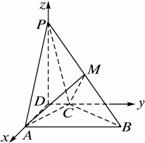
(1)解析：建立如图所示的直角坐标系D—xyz,

∵∠D=∠DAB=90°,AB=4,CD=1,AD=2,

∴A(2,0,0),C(0,1,0),B(2,4,0).

由PD⊥平面ABCD，得∠PAD为PA与平面ABCD所成的角.∴∠PAD=60°.

在Rt△PAD中，由AD=2，得PD=23.

∴P(0,0,23).

(2)解析：∵=(2,0,-2), =(-2,-3,0),

∴cos〈,〉==-.

∴PA与BC所成的角为arccos.

(3)证明：∵M为PB的中点，

∴点M的坐标为(1,2,).

∴=(-1,2,), =(1,1,),PB=(2,4,-2).

∵·=(-1)×2+2×4+×(-2)=0,

·=1×2+1×4+3×(-2)=0,?

∴⊥,⊥.

∴PB⊥平面AMC.

又PB面PCB,

∴平面AMC⊥平面PBC.