
【题目】尧盛机械生产厂每生产某产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为
(万元),其中固定成本为![]() 万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入
万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入![]() (万元)满足
(万元)满足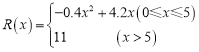 ,假定生产的产品都能卖掉,请完成下列问题:
,假定生产的产品都能卖掉,请完成下列问题:
(1)写出利润函数![]() 的解析式(注:利润=销售收入-总成本);
的解析式(注:利润=销售收入-总成本);
(2)试问该工厂生产多少台产品时,可使盈利最多?
 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】观察以下5个等式:
-1=-1
-1+3=2
-1+3-5=-3
-1+3-5+7=4
-1+3-5+7-9=-5
……
根据以上式子规律:
(1)写出第6个等式,并猜想第n个等式;(n∈N*)
(2)用数学归纳法证明上述所猜想的第n个等式成立.(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是村里一个小湖的一角,其中
是村里一个小湖的一角,其中![]() . 为了给村民营造丰富的休闲环境,村委会决定在直线湖岸
. 为了给村民营造丰富的休闲环境,村委会决定在直线湖岸![]() 与
与![]() 上分别建观光长廊
上分别建观光长廊![]() 与
与![]() ,其中
,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米;
元/米;![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米;两段长廊的总造价预算为
元/米;两段长廊的总造价预算为![]() 万元(恰好都用完);同时,在线段
万元(恰好都用完);同时,在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个表演舞台,并建水上通道
处建一个表演舞台,并建水上通道![]() (表演舞台的大小忽略不计),水上通道的造价是
(表演舞台的大小忽略不计),水上通道的造价是![]() 元/米.
元/米.

(1)若规划宽长廊![]() 与窄长廊
与窄长廊![]() 的长度相等,则水上通道
的长度相等,则水上通道![]() 的总造价需多少万元?
的总造价需多少万元?
(2)如何设计才能使得水上通道![]() 的总造价最低?最低总造价是多少万元?
的总造价最低?最低总造价是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(重点班)我们知道对数函数![]() ,对任意
,对任意![]() ,都有
,都有![]() 成立,若
成立,若![]() ,则当
,则当![]() 时,
时,![]() .参照对数函数的性质,研究下题:定义在
.参照对数函数的性质,研究下题:定义在![]() 上的函数
上的函数![]() 对任意
对任意![]() ,都有
,都有![]() ,并且当且仅当
,并且当且仅当![]() 时,
时,![]() 成立.
成立.
(1)设![]() ,求证:
,求证:![]() ;
;
(2)设![]() ,若
,若![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.

(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】p:x≠2或y≠3;q:x+y≠5,则( )
A.p是q的充分非必要条件
B.p是q的必要非充分条件
C.p是q的充要条件
D.p既不是q的充分条件,也不是q的必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com