[题目]设不等式﹣2＜|x﹣1|﹣|x+2|＜0的解集为M.a.b∈M.(1)证明:| a+ b|＜ ,(2)比较|1﹣4ab|与2|a﹣b|的大小.并说明理由．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】设不等式﹣2＜|x﹣1|﹣|x+2|＜0的解集为M，a、b∈M，
（1）证明：| a+ b|＜；
（2）比较|1﹣4ab|与2|a﹣b|的大小，并说明理由．

【答案】
（1）解：记f（x）=|x﹣1|﹣|x+2|= ，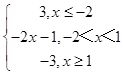

由﹣2＜﹣2x﹣1＜0解得﹣ ＜x＜，则M=（﹣ ，）．

∵a、b∈M，∴ ，

所以| a+ b|≤ |a|+ |b|＜ × + × =

（2）解：由（1）得a2＜，b2＜．

因为|1﹣4ab|2﹣4|a﹣b|2=（1﹣8ab+16a2b2）﹣4（a2﹣2ab+b2）

=（4a2﹣1）（4b2﹣1）＞0，

所以|1﹣4ab|2＞4|a﹣b|2，故|1﹣4ab|＞2|a﹣b|

【解析】（1）利用绝对值不等式的解法求出集合M，利用绝对值三角不等式直接证明：| a+ b|＜；（2）利用（1）的结果，说明ab的范围，比较|1﹣4ab|与2|a﹣b|两个数的平方差的大小，即可得到结果．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】实数a，b满足ab＞0且a≠b，由a、b、、按一定顺序构成的数列（）
A.可能是等差数列，也可能是等比数列
B.可能是等差数列，但不可能是等比数列
C.不可能是等差数列，但可能是等比数列
D.不可能是等差数列，也不可能是等比数列

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知全集为R，集合A={x|x2﹣2x＞0}，B={x|1＜x＜3}，则RB= ， A∩B= ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）= +acosx，g（x）是f（x）的导函数．
（1）若f（x）在处的切线方程为y= ，求a的值；
（2）若a≥0且f（x）在x=0时取得最小值，求a的取值范围；
（3）在（1）的条件下，当x＞0时，．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列{an}是公差不为0的等差数列，Sn为数列{an}的前n项和，S5=20，a1 ， a3 ， a7成等比数列．
（1）求数列{an}的通项公式；
（2）若bn+1=bn+an ，且b1=1，求数列{ }的前n项和Tn ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AB⊥AD，AD∥BC，AD= BC=2，E在BC上，且BE= AB=1，侧棱PA⊥平面ABCD．
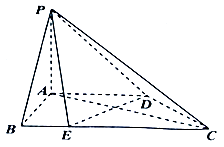
（1）求证：平面PDE⊥平面PAC；
（2）若△PAB为等腰直角三角形．（i）求直线PE与平面PAC所成角的正弦值；
（ii）求二面角A﹣PC﹣D的余弦值．