Question

11．已知抛物线y²=2x上的动点，又有点A（3，$\frac{10}{3}$），求|PA|+|PF|的最小值为$\frac{25}{6}$．

Answer 1

分析 由于点A在抛物线的外边，因此连接FA与抛物线相交于点P（2，2）即为所求．

解答 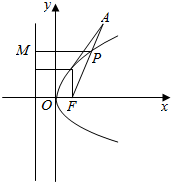解：如图所示，F（$\frac{1}{2}$，0），
可得直线FA：y=$\frac{\frac{10}{3}}{3-\frac{1}{2}}$（x-$\frac{1}{2}$），化为4x-3y-2=0，
与抛物线联立，解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{1}{8}}\\{y=-\frac{1}{2}}\end{array}\right.$．
由于点A在抛物线的外边，
因此连接FA与抛物线相交于点P（2，2）．
则取点P（2，2）时，|PA|+|PF|取得最小值|FA|=$\sqrt{（3-\frac{1}{2}）^{2}+（\frac{10}{3}）^{2}}$=$\frac{25}{6}$．
故答案为：$\frac{25}{6}$．

点评 本题考查了抛物线的标准方程及其性质，考查了推理能力与计算能力，属于中档题．