
【题目】已知三点O(0,0),A(﹣2,1),B(2,1),曲线C上任意一点M(x,y)满足| ![]() +
+ ![]() |=
|= ![]() (
( ![]() +
+ ![]() )+2.
)+2.
(1)求曲线C的方程;
(2)动点Q(x0 , y0)(﹣2<x0<2)在曲线C上,曲线C在点Q处的切线为直线l:是否存在定点P(0,t)(t<0),使得l与PA,PB都相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值.若不存在,说明理由.
【答案】
(1)解:由 ![]() =(﹣2﹣x,1﹣y),
=(﹣2﹣x,1﹣y), ![]() =(2﹣x,1﹣y)可得
=(2﹣x,1﹣y)可得 ![]() +
+ ![]() =(﹣2x,2﹣2y),
=(﹣2x,2﹣2y),
∴| ![]() +
+ ![]() |=
|= ![]() ,
, ![]() (
( ![]() +
+ ![]() )+2=(x,y)(0,2)+2=2y+2.
)+2=(x,y)(0,2)+2=2y+2.
由题意可得 ![]() =2y+2,化简可得 x2=4y.
=2y+2,化简可得 x2=4y.
(2)解:假设存在点P(0,t)(t<0),满足条件,则直线PA的方程是y= ![]() ,直线PB的方程是y=
,直线PB的方程是y= ![]()
∵﹣2<x0<2,∴ ![]()
①当﹣1<t<0时, ![]() ,存在x0∈(﹣2,2),使得
,存在x0∈(﹣2,2),使得 ![]()
∴l∥PA,∴当﹣1<t<0时,不符合题意;
②当t≤﹣1时, ![]() ,
, ![]() ,
,
∴l与直线PA,PB一定相交,分别联立方程组
 ,
, 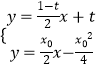 ,解得D,E的横坐标分别是
,解得D,E的横坐标分别是 ![]() ,
, ![]()
∴ ![]()
∵|FP|=﹣ ![]()
∴ ![]() =
= ![]()
∵ ![]()
∴ ![]() ×
× ![]()
∵x0∈(﹣2,2),△QAB与△PDE的面积之比是常数
∴ ![]() ,解得t=﹣1,
,解得t=﹣1,
∴△QAB与△PDE的面积之比是2.
【解析】(1)用坐标表示 ![]() ,
, ![]() ,从而可得
,从而可得 ![]() +
+ ![]() ,可求|
,可求| ![]() +
+ ![]() |,利用向量的数量积,结合M(x,y)满足|
|,利用向量的数量积,结合M(x,y)满足| ![]() +
+ ![]() |=
|= ![]() (
( ![]() +
+ ![]() )+2,可得曲线C的方程;(2)假设存在点P(0,t)(t<0),满足条件,则直线PA的方程是y=
)+2,可得曲线C的方程;(2)假设存在点P(0,t)(t<0),满足条件,则直线PA的方程是y= ![]() ,直线PB的方程是y=
,直线PB的方程是y= ![]() 分类讨论:①当﹣1<t<0时,l∥PA,不符合题意;②当t≤﹣1时,
分类讨论:①当﹣1<t<0时,l∥PA,不符合题意;②当t≤﹣1时, ![]() ,
, ![]() ,分别联立方程组,解得D,E的横坐标,进而可得△QAB与△PDE的面积之比,利用其为常数,即可求得结论.
,分别联立方程组,解得D,E的横坐标,进而可得△QAB与△PDE的面积之比,利用其为常数,即可求得结论.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为集合A,B={x|x<a}.
的定义域为集合A,B={x|x<a}.
(1)求集合A;
(2)若AB,求a的取值范围;
(3)若全集U={x|x≤4},a=-1,求U A及A∩(U B).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每一天下雨的概率均为40%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,这三天中恰有两天下雨的概率近似为
A.0.35 B.0.25 C.0.20 D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1 , l2分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明AR∥FQ;
(2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面命题中,正确的命题有( )
①若n1,n2分别是不同平面α,β的法向量,则n1∥n2α∥β;
②若n1,n2分别是平面α,β的法向量,则α⊥βn1·n2=0;
③若n是平面α的法向量,b,c是α内两个不共线的向量,a=λb+μc(λ,μ∈R),则n·a=0;
④若两个平面的法向量不垂直,则这两个平面一定不垂直.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①若函数![]() 在区间
在区间![]() 上单调递增,则
上单调递增,则![]() ;
;
②若![]() (
(![]() 且
且![]() ),则
),则![]() 的取值范围是
的取值范围是![]() ;
;
③若函数![]() ,则对任意的
,则对任意的![]() ,都有
,都有![]() ;
;
④若![]() (
(![]() 且
且![]() ),在区间
),在区间![]() 上单调递减,则
上单调递减,则![]() .
.
其中所有正确命题的序号是______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E,F分别是AB,PD的中点,若PA=AD=3,CD=![]()
①求证:AF∥平面PCE
②求证:平面PCE⊥平面PCD
③求直线FC与平面PCE所成角的正弦值.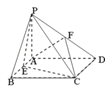
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.![]() 年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本
年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本![]() 万元,每生产
万元,每生产![]() (百辆),需另投入成本
(百辆),需另投入成本![]() 万元,且
万元,且 .由市场调研知,每辆车售价
.由市场调研知,每辆车售价![]() 万元,且全年内生产的车辆当年能全部销售完.
万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (百辆)的函数关系式;(利润=销售额-成本)
(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com