
【题目】如图,平行四边形![]() 所在平面与直角梯形
所在平面与直角梯形![]() 所在平面互相垂直,且
所在平面互相垂直,且![]() ,
,![]() 为
为![]() 中点.
中点.
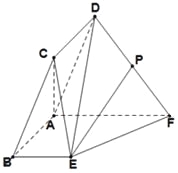
(1)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(2)求平面![]() 与平面
与平面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,底面ABCD是等腰梯形,
中,底面ABCD是等腰梯形,![]() ,
,![]() ,
,![]() ,顶点
,顶点![]() 在底面ABCD内的射影恰为点C.
在底面ABCD内的射影恰为点C.

(1)求证:BC⊥平面ACD1;
(2)若直线DD1与底面ABCD所成的角为![]() ,求平面
,求平面![]() 与平面ABCD所成锐二面角的余弦值.
与平面ABCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() 函数
函数![]() .
.
(1)将函数![]() 的图像向右平移m(
的图像向右平移m(![]() )个单位长度,所得图像对应的函数为奇函数,写出m的最小值(不要求写过程);
)个单位长度,所得图像对应的函数为奇函数,写出m的最小值(不要求写过程);
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() (
(![]() )在区间
)在区间![]() 上是单调递增函数,求正数
上是单调递增函数,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查;②运动会的工作人员为参加![]() 接力赛的6支队伍安排跑道;③一次数学月考中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人有解有关情况.针对这三个事件,恰当的抽样方法分别为( )
接力赛的6支队伍安排跑道;③一次数学月考中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人有解有关情况.针对这三个事件,恰当的抽样方法分别为( )
A.分层抽样、分层抽样、简单随机抽样B.系统抽样、简单随机抽样、分层抽样
C.简单随机抽样、简单随机抽样、分层抽样D.系统抽样、分层抽样、简单随机抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() :
:![]() =0(a>0),曲线
=0(a>0),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系;
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系;
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)已知极坐标方程为![]() =
=![]() 的直线与曲线
的直线与曲线![]() ,
,![]() 分别相交于P,Q两点(均异于原点O),若|PQ|=
分别相交于P,Q两点(均异于原点O),若|PQ|=![]() ﹣1,求实数a的值;
﹣1,求实数a的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com