
| f(x 2)-f(x 1) |
| x 2-x 1 |
| f(x 2)-f(x 1) |
| x 2-x 1 |
| f(x 2)-f(x 1) |
| x 2-x 1 |
| f(x 2)-f(x 1) |
| x 2-x 1 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:江西省修水一中2011届高三第一次月考理科数学试题 题型:013
对于正实数α,记Mα为满足下述条件的函数f(x)构成的集合:![]() x1,x2∈R且x2>x1,有-α(x2-x1)<f(x2)-f(x1)<α(x2-x1).下列结论中正确的是
x1,x2∈R且x2>x1,有-α(x2-x1)<f(x2)-f(x1)<α(x2-x1).下列结论中正确的是
若f(x)∈Mα1,g(x)∈Mα2,则f(x)·g(x)∈Mα1·α2
若f(x)∈Mα1,g(x)∈Mα2,且g(x)≠0,则![]() ∈
∈![]()
若f(x)∈Mα1,g(x)∈Mα2,则f(x)+g(x)∈Mα1+α2
若f(x)∈Mα1,g(x)∈Mα2,且α1>α2,则f(x)-g(x)∈Mα1-α2
查看答案和解析>>
科目:高中数学 来源:四川省绵阳南山中学2011届高三九月月考理科数学试题 题型:013
对于正实数α,记Mα为满足下述条件的函数f(x)构成的集合:对任意实数x1、x2且x2>x1,都有-α(x2-x1)<f(x2)-f(x1)<α(x2-x1).下列结论中正确的是
若f(x)∈Mα1,g(x)∈Mα2,则f(x)·g(x)∈Mα1·α2
若f(x)∈Mα1,g(x)∈Mα2,则f(x)+g(x)∈Mα1+α2
若f(x)∈Mα1,g(x)∈Mα2,且g(x)≠0,则![]() ∈
∈![]()
若f(x)∈Mα1,g(x)∈Mα2,且α1>α2,则f(x)-g(x)∈Mα1-α2
查看答案和解析>>
科目:高中数学 来源:江西省09-10学年高二下学期第二次段考数学文科试卷 题型:选择题
对于正实数α,记Mα为满足下述条件的函数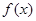 构成的集合:存在
构成的集合:存在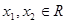 ,且
,且 ,有
,有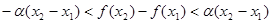 ,下列结论中正确的是( )
,下列结论中正确的是( )
A.若 ,则
,则
B.若 ,且
,且 ,则
,则
C.若 ,则
,则
D.若 ,且
,且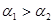 ,则
,则
查看答案和解析>>
科目:高中数学 来源:浙江省高考真题 题型:单选题
对于正实数α,记Mα为满足下述条件的函数f(x)构成的集合: x1,x2∈R且x2>x1,有-α(x2-x1)<f(x2)- f(x1)<α(x2-x1)下列结论中正确的是
x1,x2∈R且x2>x1,有-α(x2-x1)<f(x2)- f(x1)<α(x2-x1)下列结论中正确的是
 ,g(x)∈
,g(x)∈ ,则f(x)·g(x)∈
,则f(x)·g(x)∈
 ,g(x)∈
,g(x)∈ ,且g(x)≠0 则
,且g(x)≠0 则
 ,g(x)∈
,g(x)∈ ,则f(x)+g(x)∈
,则f(x)+g(x)∈
 ,g(x)∈
,g(x)∈ ,且α1>α2,则f(x)-g(x)∈
,且α1>α2,则f(x)-g(x)∈
查看答案和解析>>
科目:高中数学 来源:江西省新余一中09-10学年高二下学期第二次段考数学文科试卷 题型:单选题
对于正实数α,记Mα为满足下述条件的函数 构成的集合:存在
构成的集合:存在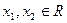 ,且
,且 ,有
,有 ,下列结论中正确的是( )
,下列结论中正确的是( )
A.若 ,则 ,则 |
B.若 ,且 ,且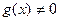 ,则 ,则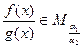 |
C.若 ,则 ,则 |
D.若 ,且 ,且 ,则 ,则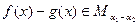 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com