
已知函数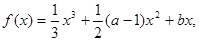 (
(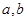 为常数)在
为常数)在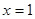 和
和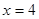 处取得极值,
处取得极值,
(1)求函数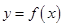 的解析式;
的解析式;
(2)当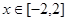 时,
时,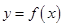 的图像恒在直线
的图像恒在直线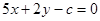 的下方,求实数
的下方,求实数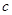 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
(06年天津卷理)已知函数![]() 、
、![]() 为常数,
为常数,![]() 在
在![]() 处取得最小值,则函数
处取得最小值,则函数![]() 是
是
(A)偶函数且它的图象关于点![]() 对称 (B)偶函数且它的图象关于点
对称 (B)偶函数且它的图象关于点![]() 对称
对称
(C)奇函数且它的图象关于点![]() 对称 (D)奇函数且它的图象关于点
对称 (D)奇函数且它的图象关于点![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源:2014届辽宁丹东市高二4月月考(一)理科数学试卷(解析版) 题型:选择题
已知函数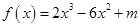 (
(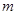 为常数)在
为常数)在 上有最大值3,那么此函数在
上有最大值3,那么此函数在 上的最小值为( )
上的最小值为( )
A.-29 B.-37 C.-5 D.-1
查看答案和解析>>
科目:高中数学 来源:2010年漳州市高二下学期期末考试理科数学卷 题型:解答题
(本小题满分14分)已知函数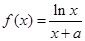 (
( 为常数)在点
为常数)在点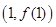 处
处
切线的斜率为 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若函数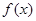 在区间
在区间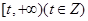 上存在极值,求
上存在极值,求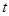 的最大值;
的最大值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com