
【题目】如图,![]() 为椭圆
为椭圆![]() 的左右焦点,
的左右焦点,![]() 是椭圆的两个顶点,
是椭圆的两个顶点,![]() ,
,![]() ,若点
,若点![]() 在椭圆
在椭圆![]() 上,则点
上,则点![]() 称为点
称为点![]() 的一个“椭点”.直线
的一个“椭点”.直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 两点的“椭点”分别为
两点的“椭点”分别为![]() ,已知以
,已知以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() .
.
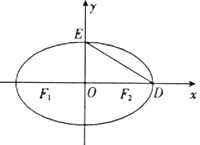
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试探讨![]() 的面积
的面积![]() 是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 的面积为定值1.
的面积为定值1.
【解析】
试题分析:(1)要求椭圆标准方程,一般要找到两个关于![]() 的等式,由椭圆的几何性质,题中两个线段长正好提供了两个等式,一个
的等式,由椭圆的几何性质,题中两个线段长正好提供了两个等式,一个![]() ,即为
,即为![]() ,
,![]() ,即为
,即为![]() ,再由
,再由![]() ,可得
,可得![]() 值;(2)本小题是定值问题的研究,首先设
值;(2)本小题是定值问题的研究,首先设![]() ,
,![]() ,写出“椭圆点”坐标
,写出“椭圆点”坐标![]() ,
,![]() .由已知可得它们的关系:
.由已知可得它们的关系:![]() .接着考虑直线
.接着考虑直线![]() ,分类讨论斜率不存在,以及斜率存在两种情形,对斜率不存在的特殊情形可直接求出点
,分类讨论斜率不存在,以及斜率存在两种情形,对斜率不存在的特殊情形可直接求出点![]() 坐标,对斜率存在时,可设
坐标,对斜率存在时,可设![]() 方程为
方程为![]() ,代入椭圆方程后可得
,代入椭圆方程后可得![]() ,从而得
,从而得![]() ,代入
,代入![]() 得
得![]() 的关系式,此时可验证下判别式
的关系式,此时可验证下判别式![]() ,由直线与椭圆相交的弦长公式求得
,由直线与椭圆相交的弦长公式求得![]() ,由点到直线距离公式可求得
,由点到直线距离公式可求得![]() 上的高,从而求得
上的高,从而求得![]() .
.
试题解析:(1)由题可得 解得
解得 ,故椭圆
,故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设![]() ,
,![]() ,则
,则![]() ,
,![]() .由
.由![]() ,即
,即![]() .(*)
.(*)
①当直线![]() 的斜率不存在时,
的斜率不存在时,![]() .
.
②当直线![]() 的斜率存在时,设其直线为
的斜率存在时,设其直线为![]() ,联立
,联立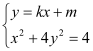 得
得
![]() ,则
,则![]() ,
,![]() ,同理
,同理![]() ,代入(*),整理得
,代入(*),整理得![]() ,此时
,此时![]() ,
, ,∴
,∴![]() .
.
综上,![]() 的面积为定值1.
的面积为定值1.


科目:高中数学 来源: 题型:
【题目】如果事件A与B是互斥事件且事件A+B的概率是0.8,事件A的概率是事件B的概率的3倍,则事件A的概率是( )
A.0.4
B.0.6
C.0.8
D.0.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用输入语句可以给多个变量赋值,下面能实现这一功能的语句是( )
A.INPUT “A,B,C”a,b,c
B.INPUT “A,B,C=”;a,b,c
C.INPUT a,b,c;“A,B,C”
D.PRINT “A,B,C”;a,b,c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图(如图),其中上面的折线代表可能出现的从高气温,下面的折线代表可能出现的最低气温.
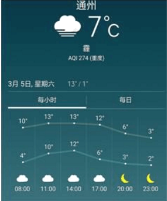
(Ⅰ)指出最高气温与最低气温的相关性;
(Ⅱ)比较最低气温与最高气温方差的大小(结论不要求证明);
(Ⅲ)在![]() 内每个整点时刻的温差(最高气温与最低气温的差)依次记为
内每个整点时刻的温差(最高气温与最低气温的差)依次记为![]() ,求
,求
在连续两个时刻的温差中恰好有一个时刻的温差不小于![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com