
 下表是关于某设备的使用年限(年)和所需要的维修费用y(万元)的几组统计数据:
下表是关于某设备的使用年限(年)和所需要的维修费用y(万元)的几组统计数据:| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
分析 (1)由题意易得散点图:
(2)由已知数据求出$\overline{x}$=4,$\overline{y}$=5,$\sum_{i=1}^{5}{{x}_{i}}^{2}$=90,结合参考数据可得$\widehat{b}$和$\widehat{a}$,可得回归直线方程;
(3)把x=10代入(2)中的方程计算可得;
解答 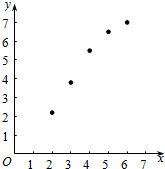 解:(1)由题意可得散点图如图:
解:(1)由题意可得散点图如图:
(2)从散点图可知,变量y与x之间有较强的线性相关性.
由已知数据有:$\overline{x}$=4,$\overline{y}$=5,$\sum_{i=1}^{5}{{x}_{i}}^{2}$=90,
又由参考数据知$\sum_{i=1}^{5}{x}_{i}{y}_{i}=112.3$
∴$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{112.3-5×4×5}{90-5×{4}^{2}}$=1.23,
∴$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=5-1.23×4=0.08,
∴回归直线方程为$\widehat{y}$=1.23x+0.08;
(3)当x=10时,维修费用$\widehat{y}$=1.23×10+0.08=12.38(万元)
点评 本题考查线性回归方程,考查学生的计算能力,属基础题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
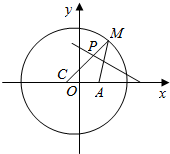 已知圆C:(x+1)2+y2=25,定点A(1,0),M为圆上的一个动点,连接MA,作MA的垂直平分线交半径MC于P,当M点在圆周上运动时,点P的轨迹方程为$\frac{{x}^{2}}{\frac{25}{4}}+\frac{{y}^{2}}{\frac{21}{4}}=1$.
已知圆C:(x+1)2+y2=25,定点A(1,0),M为圆上的一个动点,连接MA,作MA的垂直平分线交半径MC于P,当M点在圆周上运动时,点P的轨迹方程为$\frac{{x}^{2}}{\frac{25}{4}}+\frac{{y}^{2}}{\frac{21}{4}}=1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com