(1)证明:∵f(xy)=f(x)+f(y),∴
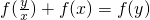
,
∴
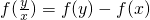
;
(2)解:∵f(x
1)<f(x
2),∴f(x
1)-f(x
2)<0,
又
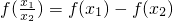
,所以
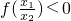
∵当且仅当x>1时,f(x)<0成立,∴当f(x)<0时,x>1,
∴

,x
1>x
2(3)解:令x=y=1代入f(xy)=f(x)+f(y)得f(1)=f(1)+f(1),f(1)=0,
∴f(x
2-2x+1)>0?f(x
2-2x+1)>f(1),
由(2)可知函数f(x)在定义域(0,+∞)上是减函数,
∴0<x
2-2x+1<1,
解得0<x<2且x≠1,
∴不等式解集为(0,1)∪(1,2)
分析:(1)取y=

,代入已知等式即可证得结果;
(2)由f(x
1)<f(x
2),结合(1)中等式
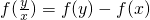
,得到
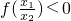
,再根据当且仅当x>1时,f(x)<0成立得到

,从而得到x
1>x
2;
(3)在已知等式中取特值x=y=1求出f(1)=0,由(2)可知函数f(x)在定义域(0,+∞)上是减函数,在不等式f(x
2-2x+1)>0中,用f(1)替换0后利用函数的单调性脱掉“f”,则不等式的解集可求.
点评:本题考查了抽象函数的应用,考查了函数的单调性的判断与证明,训练了特值法求函数的值,考查了学生灵活处理问题和解决问题的能力,属中档题.

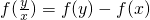 ;
;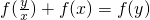 ,
,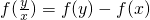 ;
;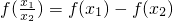 ,所以
,所以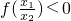
 ,x1>x2
,x1>x2 ,代入已知等式即可证得结果;
,代入已知等式即可证得结果;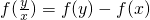 ,得到
,得到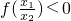 ,再根据当且仅当x>1时,f(x)<0成立得到
,再根据当且仅当x>1时,f(x)<0成立得到 ,从而得到x1>x2;
,从而得到x1>x2;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案