
分析 (1)由椭圆的离心率为$\frac{{\sqrt{2}}}{2}$,过点$(1,\frac{{\sqrt{2}}}{2})$,求出a,b,由此能求出椭圆的方程.
(2)当直线l的斜率存在时,设其方程为y=kx+m,代入椭圆方程,得(2k2+1)x2+4kmx+2m2-2=0,由根的判别式求出m2=2k2+1,由此能求出存在两个定点M1(1,0),M2(-1,0),使它们到直线l的距离之积等于1.
解答 (本题满分13分)
解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,
∴a2=2c2,a2=2b2,又过点$(1,\frac{{\sqrt{2}}}{2})$,…(2分)
∴$\frac{1}{a^2}+\frac{1}{{2{b^2}}}=1⇒\frac{1}{{2{b^2}}}+\frac{1}{{2{b^2}}}=1⇒{b^2}=1$
∴a2=2,
故所求椭圆的方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.…(5分)
(2)当直线l的斜率存在时,设其方程为y=kx+m,
代入椭圆方程,消去y,
整理得(2k2+1)x2+4kmx+2m2-2=0,(*)
方程(*)有且只有一个实根,又2k2+1>0,
所以△=16k2m2-4(2k2+1)(2m2-2)=0,整理,得m2=2k2+1,…(8分)
假设存在M1(λ1,0),M2(λ2,0)满足题设,
则由d1•d2=$\frac{|({λ}_{1}k+m)({λ}_{2}k+m)|}{{k}^{2}+1}$=$\frac{|{λ}_{1}{λ}_{2}{k}^{2}+({λ}_{1}+{λ}_{2})km+2{k}^{2}+1|}{{k}^{2}+1}$
=$\frac{|({λ}_{1}{λ}_{2}+2){k}^{2}+({λ}_{1}+{λ}_{2})km+1|}{{k}^{2}+1}$对任意的实数k恒成立,
所以,$\left\{\begin{array}{l}{{λ}_{1}{λ}_{2}+2=1}\\{{λ}_{1}+{λ}_{2}=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{{λ}_{1}=1}\\{{λ}_{2}=-1}\end{array}\right.$或$\left\{\begin{array}{l}{{λ}_{1}=-1}\\{{λ}_{2}=1}\end{array}\right.$,
当直线l的斜率不存在时,经检验符合题意.
综上,存在两个定点M1(1,0),M2(-1,0),使它们到直线l的距离之积等于1.…(13分)
点评 本题考查椭圆方程的求法,考查满足条件的点是否存在的判断与求法,是中档题,解题时要认真审题,注意椭圆性质、根的判别别式,韦达定理的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | m∥n,n∥α⇒m∥α | B. | α⊥β,α∩β=m,l⊥m⇒l⊥β | ||
| C. | l⊥m,l⊥n,m?α,n?α⇒l⊥α | D. | m∩n=A,m∥α,m∥β,n∥α,n∥β⇒α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ②③ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2a-1 | B. | 2-a-1 | C. | 1-2-a | D. | 1-2a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
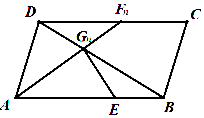 如图,已知点E为平行四边形ABCD的边AB上一点,$\overrightarrow{AE}$=2$\overrightarrow{EB}$,Fn(n∈N*)为边DC上的一列点,连接AFn交BD于Gn,点Gn(n∈N*)满足$\overrightarrow{{G_n}D}$=$\frac{1}{3}$an+1$\overrightarrow{{G_n}A}$-(3an+2)$\overrightarrow{{G_n}E}$,其中数列{an}是首项为1的正项数列,则a4的值为( )
如图,已知点E为平行四边形ABCD的边AB上一点,$\overrightarrow{AE}$=2$\overrightarrow{EB}$,Fn(n∈N*)为边DC上的一列点,连接AFn交BD于Gn,点Gn(n∈N*)满足$\overrightarrow{{G_n}D}$=$\frac{1}{3}$an+1$\overrightarrow{{G_n}A}$-(3an+2)$\overrightarrow{{G_n}E}$,其中数列{an}是首项为1的正项数列,则a4的值为( )| A. | 45 | B. | 51 | C. | 53 | D. | 61 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com