
【题目】已知f(x)是定义在R上的奇函数,当x≥0时f(x)=2x﹣x2 ,
(1)求f(x)的表达式;
(2)设0<a<b,当x∈[a,b]时,f(x)的值域为 ![]() ,求a,b的值.
,求a,b的值.
【答案】
(1)解:设x<0,可得﹣x>0,
∵当x≥0时f(x)=2x﹣x2,
∴f(﹣x)=﹣2x﹣(﹣x)2=﹣2x﹣x2,
∵f(x)是定义在R上的奇函数,
∴f(﹣x)=﹣f(x),
∴f(﹣x)=﹣f(x)=﹣2x﹣x2,
∴f(x)=x2+2x
∴f(x)= ![]()
(2)解:∵0<a<b,当x∈[a,b]时,当x≥0时f(x)=2x﹣x2=﹣(x﹣1)2+1
f(x)在(0,1)上是增函数,在(1,+∞)上是减函数,
若0<a<b<1,可得值域为[2a﹣a2,2b﹣b2],
f(x)的值域为 ![]() ,∴
,∴ 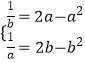 解得a=b=1,(舍去)
解得a=b=1,(舍去)
若1<a<b,可得值域为[2b﹣b2,2a﹣a2],f(x)的值域为 ![]() ,
,
∴ 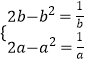 ,解得a=b=1,
,解得a=b=1,
若0<a≤1≤b,可得x=1处取得最大值,f(x)max=f(1)=2﹣1=1,
最小值在x=a或x=b处取得,
∵当x∈[a,b]时,f(x)的值域为 ![]() ,
,
∴ ![]() =1,可得a=1,
=1,可得a=1,
若 ![]() =2a﹣a2,可得b=1(舍去);
=2a﹣a2,可得b=1(舍去);
若 ![]() =2b﹣b2,化简得(b﹣1)(b2﹣b﹣1)=0解得b1=
=2b﹣b2,化简得(b﹣1)(b2﹣b﹣1)=0解得b1= ![]() ,b2=
,b2= ![]() (舍去),
(舍去),
∴a=1,b= ![]()
【解析】(1)由题意设x<0,得﹣x>0利用已知的解析式求出f(﹣x)=﹣x2﹣2x,再由f(x)=﹣f(﹣x),求出f(x)时的解析式.(2)因为0<a<b,利用配方法,可以证明f(x)在x>0时的单调性,需要分类讨论,再对其进行求解;
【考点精析】本题主要考查了函数的定义域及其求法和函数的值域的相关知识点,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】函数f(x)=ln(3﹣x)(x+1)的定义域为( )
A.[﹣1,3]
B.(﹣1,3)
C.(﹣∞,﹣3)∪(1,+∞)
D.(﹣∞,﹣1)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程 ![]() =
= ![]() x+
x+ ![]() 的
的 ![]() 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元
B.65.5万元
C.67.7万元
D.72.0万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2sin4x+2cos4x+cos22x﹣3.
(1)求函数f(x)的最小正周期.
(2)求函数f(x)在闭区间[ ![]() ]上的最小值并求当f(x)取最小值时,x的取值集合.
]上的最小值并求当f(x)取最小值时,x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年6月22 日,“国际教育信息化大会”在山东青岛开幕.为了解哪些人更关注“国际教育信息化大会”,某机构随机抽取了年龄在15-75岁之间的100人进行调查,经统计“青少年”与“中老年”的人数之比为9: 11.
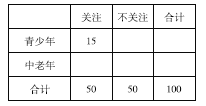
(1)根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查.在这9人中再选取3人进行面对面询问,记选取的3人中关注“国际教育信息化大会”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:参考公式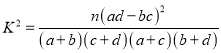 ,其中
,其中![]() .
.
临界值表:
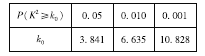
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为( ![]() ,0),求θ的最小值.
,0),求θ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com