
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的半径为2,圆心在
的半径为2,圆心在![]() 轴的正半轴上,且与直线
轴的正半轴上,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程。
的方程。
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,且△
,且△![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标及对应的△
的坐标及对应的△![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】若点O在![]() 内,且满足
内,且满足![]() ,设
,设![]() 为
为![]() 的面积,
的面积, ![]() 为
为![]() 的面积,则
的面积,则![]() =________.
=________.
【答案】![]()
【解析】由![]() ,可得:
,可得: ![]()
延长OA,OB,OC,使OD=2OA,OE=4OB,OF=3OC,
如图所示:

∵2![]() +3
+3![]() +4
+4![]() =
=![]() ,
,
∴![]() ,
,
即O是△DEF的重心,
故△DOE,△EOF,△DOF的面积相等,
不妨令它们的面积均为1,
则△AOB的面积为![]() ,△BOC的面积为
,△BOC的面积为![]() ,△AOC的面积为
,△AOC的面积为![]() ,
,
故三角形△AOB,△BOC,△AOC的面积之比依次为: ![]() :
: ![]() :
: ![]() =3:2:4,
=3:2:4,
![]() .
.
故答案为: ![]() .
.
点睛:本题考查的知识点是三角形面积公式,三角形重心的性质,平面向量在几何中的应用,注意重要结论:点O在![]() 内,且满足
内,且满足![]() ,
, ![]() 则三角形△AOB,△BOC,△AOC的面积之比依次为:
则三角形△AOB,△BOC,△AOC的面积之比依次为: ![]() .
.
【题型】填空题
【结束】
16
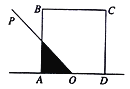
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记![]() 为
为![]() OP所经过的在正方形ABCD内的区域(阴影部分)的面积
OP所经过的在正方形ABCD内的区域(阴影部分)的面积![]() ,那么对于函数
,那么对于函数![]() 有以下三个结论:
有以下三个结论:
①![]() ;
;
②任意![]() ,都有
,都有![]() ;
;
③任意![]() 且
且![]() ,都有
,都有![]() .
.
其中正确结论的序号是__________. (把所有正确结论的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的通项公式为
的通项公式为![]() (
(![]() ,
, ![]() ),数列
),数列![]() 定义如下:对于正整数
定义如下:对于正整数![]() ,
, ![]() 是使得不等式
是使得不等式![]() 成立的所有
成立的所有![]() 中的最小值.
中的最小值.
(1)若![]() ,
, ![]() ,求
,求![]() ;
;
(2)若![]() ,
, ![]() ,求数列
,求数列![]() 的前
的前![]() 项和公式;
项和公式;
(3)是否存在![]() 和
和![]() ,使得
,使得![]()
![]() ?如果存在,求
?如果存在,求![]() 和
和![]() 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.718 28…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,证明:e﹣2<a<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过椭圆 ![]() =1的右焦点F作斜率k=﹣1的直线交椭圆于A,B两点,且
=1的右焦点F作斜率k=﹣1的直线交椭圆于A,B两点,且 ![]() 共线.
共线.
(1)求椭圆的离心率;
(2)当三角形AOB的面积S△AOB= ![]() 时,求椭圆的方程.
时,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )的最大值为
)的最大值为![]() ,最小值为
,最小值为![]() .
.
(1)求![]() 的值;
的值;
(2)将函数![]() 图象向右平移
图象向右平移![]() 个单位后,再将图象上所有点的纵坐标扩大到原来的
个单位后,再将图象上所有点的纵坐标扩大到原来的![]() 倍,横坐标不变,得到函数
倍,横坐标不变,得到函数![]() 的图象,求方程
的图象,求方程![]() 的解.
的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为 ![]() +
+ ![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线 ![]() ﹣
﹣ ![]() =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 ![]() .
.
(1)求椭圆C的方程;
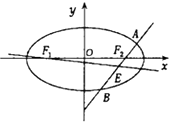
(2)设F1 , F2分别为椭圆C的左,右焦点,过F2作直线l(与x轴不重合)交于椭圆于A,B两点,线段AB的中点为E,记直线F1E的斜率为k,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有六间不同的电脑室,每天晚上至少开放两间,欲求不同安排方案的种数,现有3位同学分别给出了下列三个结果:① ![]() ;②26-7;③
;②26-7;③ ![]() ,其中正确的结论是( )
,其中正确的结论是( )
A.仅有①
B.仅有②
C.②与③
D.仅有③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com