
【题目】某校开设的校本课程分别有人文科学、自然科学、艺术体育三个课程类别,每种课程类别开设课程数及学分设定如下表所示:
人文科学类 | 自然科学类 | 艺术体育类 | |
课程门数 | 4 | 4 | 2 |
每门课程学分 | 2 | 3 | 1 |
学校要求学生在高中三年内从中选修3门课程,假设学生选修每门课程的机会均等.
(Ⅰ)甲至少选1门艺术体育类课程,同时乙至多选1门自然科学类课程的概率为多少?
(Ⅱ)求甲选的3门课程正好是7学分的概率;
(Ⅲ)设甲所选3门课程的学分数为X,写出X的分布列,并求出X的数学期望.
【答案】解:(Ⅰ)设甲至少选一门艺术体育类课程的事件为A, ![]() ; 乙至多选一门自然科学类课程的事件为B,
; 乙至多选一门自然科学类课程的事件为B, ![]() ;
;
则所求概率为 ![]()
(Ⅱ)甲选课程的学分可能为(3,3,1),(3,2,2),
所以甲选课程的学分正好为7学分的概率为 ![]()
(Ⅲ)X的可能取值为4,5,6,7,8,9 ![]()
![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]() ;
;
所以随机变量X的分布列为:
X | 4 | 5 | 6 | 7 | 8 | 9 |
P |
|
|
|
|
|
|
所以随机变量X的数学期望 ![]()
【解析】(I)利用互斥事件与互相独立事件的概率计算公式即可得出.(II)甲选课程的学分可能为(3,3,1),(3,2,2),利用互斥事件与互相独立事件的概率计算公式即可得出.(III)X的可能取值为4,5,6,7,8,9.利用互斥事件与互相独立事件的概率计算公式即可得出.
【考点精析】通过灵活运用离散型随机变量及其分布列,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=x2﹣ax+lnx,a∈R.
(1)当a=3时,求函数f(x)的极小值;
(2)令g(x)=x2﹣f(x),是否存在实数a,当x∈[1,e](e是自然对数的底数)时,函数g(x)取得最小值为1.若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为1的单调递增的等比数列,且满足a3 , ![]() 成等差数列.
成等差数列.
(1)求{an}的通项公式;
(2)若bn=log3(anan+1)(n∈N*),求数列{anbn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[100,110),[110,120),[120,130)三组内的学生中,用分层抽样的方法选取28人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为 . 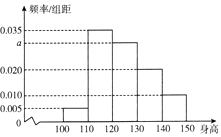
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知圆C的圆心坐标为(2,0),半径为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.,直线l的参数方程为:
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.,直线l的参数方程为: ![]() (t为参数).
(t为参数).
(1)求圆C和直线l的极坐标方程;
(2)点P的极坐标为(1, ![]() ),直线l与圆C相交于A,B,求|PA|+|PB|的值.
),直线l与圆C相交于A,B,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x)满足:f(x+1)=f(x﹣1),且当﹣1<x<0时,f(x)=2x﹣1,则f(log220)等于( )
A.![]()
B.﹣ ![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com