
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于 小于
小于 为二等品,小于
为二等品,小于 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
| 测试指标 |  |  |  |  |  |  |
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
(1) ;(2)
;(2)
解析试题分析:(1)根据上表统计得到乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.由于工人乙生产三件产品A,给工厂带来盈利大于或等于100元三种情况是:三件一等品;两件一等品,一件二等品;一件一等品,两件二等品;然后分别计算它们的概率并求和.
(2)由于甲乙分别生产一件产品A给工厂带来的盈利X共有六种情况.分别求的各种情况的概率,根据数学期望公式即可得结论.
试题解析:甲生产一件产品A为一等品、二等品、三等品的概率分别为 , 3分
, 3分
乙生产一件产品A为一等品、二等品、三等品的概率分别为 6分
6分
(1)新工人乙生产三件产品A,给工厂带来盈利大于或等于100元的情形有:三件都是一等品;二件是一等品、一件是二等品或一件是一等品、二件是二等品,概率为: 8分
8分
(2))随机变量X的所有可能取值为100,80,60,40,20,-20.  ,
, ,
, ,
, ,
, ,
,
所以,随机变量 的概率分布为:
的概率分布为:
100 80 60 40 20 -20 






随机变量X的数学期望  (元) 12分
(元) 12分
考点:1.统计概率.2.数学期望的计算.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:解答题
某中学的数学测试中设置了“数学与逻辑”和“阅读与表达”两个内容,成绩分为A、B、C、D、E五个等级。某班考生两科的考试成绩的数据统计如图所示,其中“数学与逻辑”科目的成绩等级为B的考生有10人
(1)求该班考生中“阅读与表达”科目中成绩等级为A的人数;
(2)若等级A、B、C、D、E分别对应5分、4分、3分、2分、1分,该考场中有2人10分,3人9分,从这5人中随机抽取2人,求2人成绩之和为19分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校从参加高一年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.
(1)在给出的样本频率分布表中,求A,B,C,D的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.样本频率分布表如下:
| 分组 | 频数 | 频率 |
| [40,50) | 2 | 0.04 |
| [50,60) | 3 | 0.06 |
| [60,70) | 14 | 0.28 |
| [70,80) | 15[] | 0.30 |
| [80,90) | A | B |
| [90,100] | 4 | 0.08 |
| 合计 | C | D |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分 )
2013年国庆期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段 ,
, ,
, ,
, ,
, ,
, 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)此调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的中位数的估计值;
(3)若从车速在 的车辆中任抽取3辆,求抽出的3辆车中车速在
的车辆中任抽取3辆,求抽出的3辆车中车速在 的车辆数
的车辆数 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下图为某地区2012年1月到2013年1月鲜蔬价格指数的变化情况:
记 本月价格指数
本月价格指数 上月价格指数.规定:当
上月价格指数.规定:当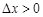 时,称本月价格指数环比增长;
时,称本月价格指数环比增长;
当 时,称本月价格指数环比下降;当
时,称本月价格指数环比下降;当 时,称本月价格指数环比持平.
时,称本月价格指数环比持平.
(1) 比较2012年上半年与下半年鲜蔬价格指数月平均值的大小(不要求计算过程);
(2) 直接写出从2012年2月到2013年1月的12个月中价格指数环比下降的月份.若从这12个月中随机选择连续的两个月进行观察,求所选两个月的价格指数都环比下降的概率;
(3)由图判断从哪个月开始连续三个月的价格指数方差最大.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高三有四个班,某次数学测试后,学校随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1)问各班被抽取的学生人数各为多少人?
(2)求平均成绩;
(3)在抽取的所有学生中,任取一名学生,求分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某城市要建成宜商、宜居的国际化现代新城,该城市的东城区、西城区分别引进8甲厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
(1)根据茎叶图判断哪个区域厂家的平均分较高;
(2)规定85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产 、
、 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:
 |  |  |  |  |  |
| B |  |  |  |  |  |
 、
、 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 、
、 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等. 与
与 的值;
的值; 件
件 种元件中任取
种元件中任取 件,求
件,求 件都为正品的概率.
件都为正品的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某食品厂对生产的某种食品按行业标准分成五个不同等级,等级系数X依次为A,B,C,D,E.现从该种食品中随机抽取20件样品进行检验,对其等级系数进行统计分析,得到频率分布表如下:
(1)在所抽取的20件样品中,等级系数为D的恰有3件,等级系数为E的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为D的3件样品记为x1,x2,x3,等级系数为E的2件样品记为y1,y2,现从x1,x2,x3,y1,y2这5件样品中一次性任取两件(假定每件样品被取出的可能性相同),试写出所有可能的结果,并求取出的两件样品是同一等级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com