
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)设u=xlnx,x∈[1,e],得到y=u2+(2t-1)u+t2-t,根据二次函数的性质求出y的最小值即可;
(Ⅲ)求出函数h(x)的导数,问题可化为h(x1)-$\frac{m}{{x}_{1}}$≤h(x2)-$\frac{m}{{x}_{2}}$,设v(x)=h(x)-$\frac{m}{x}$,根据函数的单调性求出m的范围即可.
解答 解:(Ⅰ)y=xlnx,x∈(0,+∞),y′=lnx+1,
x∈(0,$\frac{1}{e}$)时,y′<0,y=xlnx递减,
x∈($\frac{1}{e}$,+∞)时,y′>0,y=xlnx递增,
∴y=xlnx在(0,$\frac{1}{e}$)递减,在($\frac{1}{e}$,+∞)递增;
(Ⅱ)y=(xlnx+t)2-(xlnx+t)=(xlnx)2+(2t-1)xlnx+t2-t,
设u=xlnx,x∈[1,e],
由(Ⅰ)得u=xlnx在[1,e]递增,
故u∈[0,e],
此时y=u2+(2t-1)u+t2-t,
对称轴u=$\frac{1-2t}{2}$,
t∈[$\frac{1}{2}$,1],∴$\frac{1-2t}{2}$∈[-$\frac{1}{2}$,0],
u∈[0,e],故u=0时,ymin=t2-t;
(Ⅲ)h(x)=$\frac{1}{2}$x2-(2a+2)x+(2a+1)lnx,
h′(x)=$\frac{[x-(2a+1)](x-1)}{x}$,x∈[1,2],
a∈[e,3]时,2a+1∈[2e+1,7],
故h′(x)<0在[1,2]成立,
即h(x)在[1,2]递减,
∵x1≠x2,不妨设1≤x1<x2≤2,
则h(x1)>h(x2),x1<x2,
故原不等式可化为h(x1)-$\frac{m}{{x}_{1}}$≤h(x2)-$\frac{m}{{x}_{2}}$,
对1≤x1<x2≤2成立,
设v(x)=h(x)-$\frac{m}{x}$,
则v(x)在[1,2]递增,其中a∈[e,3],
即v′(x)≥0在[1,2]恒成立,
而v′(x)=$\frac{[x-(2a+1)](x-1)}{x}$+$\frac{m}{{x}^{2}}$≥0,
即x-(2a+2)+$\frac{2a+1}{x}$+$\frac{m}{{x}^{2}}$≥0恒成立,
即(2x-2x2)a+x3-2x2+x+m≥0恒成立,a∈[e,3],
由于x∈[1,2],∴2x-2x2≤0,
故只需(2x-2x2)a+x3-2x2+x+m≥0,
即x3-8x2+7x+m≥0,
令k(x)=x3-8x2+7x+m,x∈[1,2],
k′(x)=3x2-16x+7<0,
故k(x)在x∈[1,2]上递减,
∴k(x)min=k(2)=m-10≥0,
∴m≥10,
∴m∈[10,+∞).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
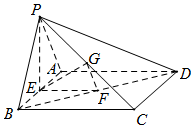 如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 中学 | 甲 | 乙 | 丙 | 丁 |
| 人数 | 30 | 40 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 8个 | C. | 9个 | D. | 10个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com