
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处切线的斜率为
处切线的斜率为![]() ,求此切线方程;
,求此切线方程;
(2)若![]() 有两个极值点
有两个极值点![]() ,求
,求![]() 的取值范围,并证明:
的取值范围,并证明:![]() .
.
【答案】(1) ![]() .
.
(2)见解析.
【解析】分析:第一问首先利用导数的几何意义以及切点既在切线上,又在函数图像上,从而利用相应的公式求得切线方程;第二问从函数有两个极值点,对应的是其导数等于零有两个不相等的正根,构造新函数,利用导数研究其走向,分类讨论证得结果.
详解:(1)∵![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
∴![]() ,故切点为
,故切点为![]() ,
,
所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(2)![]() ,令
,令![]() ,得
,得![]() .
.
令![]() ,则
,则![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
令![]() ,得
,得![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故![]() 在
在![]() 递增,在
递增,在![]() 递减,所以
递减,所以![]() .
.
所以当![]() 时,
时,![]() 有一个极值点;
有一个极值点;
![]() 时,
时,![]() 有两个极值点;
有两个极值点;
当![]() 时,
时,![]() 没有极值点.
没有极值点.
综上,![]() 的取值范围是
的取值范围是![]() .
.
因为![]() 是
是![]() 的两个极值点,所以
的两个极值点,所以![]() 即
即![]() …①
…①
不妨设![]() ,则
,则![]() ,
,![]() ,
,
因为![]() 在
在![]() 递减,且
递减,且![]() ,所以
,所以![]() ,即
,即![]() …②.
…②.
由①可得![]() ,即
,即![]() ,
,
由①,②得![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】在全国第五个“扶贫日”到来之前,某省开展“精准扶贫,携手同行”的主题活动,某贫困县调查基层干部走访贫困户数量.![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从
镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从![]() 三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,
三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
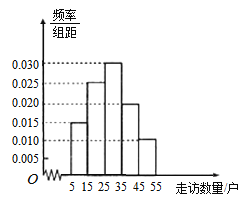
(1)求这40人中有多少人来自![]() 镇,并估计
镇,并估计![]() 三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
(2)如果把走访贫困户达到或超过25户视为工作出色,以频率估计概率,从![]() 三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为
三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,当直线垂直于
两点,当直线垂直于![]() 轴时,
轴时,![]() .
.
(1)求椭圆![]() 的方程
的方程
(2)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形?若存在,求出
为底的等腰三角形?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙二人进行乒乓球比赛,已知每一局比赛甲胜乙的概率是![]() ,假设每局比赛结果相互独立.
,假设每局比赛结果相互独立.
(Ⅰ)比赛采用三局两胜制,即先获得两局胜利的一方为获胜方,这时比赛结束.求在一场比赛中甲获得比赛胜利的概率;
(Ⅱ)比赛采用三局两胜制,设随机变量![]() 为甲在一场比赛中获胜的局数,求
为甲在一场比赛中获胜的局数,求![]() 的分布列和均值;
的分布列和均值;
(Ⅲ)有以下两种比赛方案:方案一,比赛采用五局三胜制;方案二,比赛采用七局四胜制.问哪个方案对甲更有利.(只要求直接写出结果)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长沙某公司生产一种高科技晶片100片,生产过程中由于受到一些不可抗因素的影响,晶片会受到一定程度的磨损,因此在生产结束之后需要由测试人员进行相应的指标测试.指标测试情况统计如表所示:
若![]() ,则称该晶片为合格品,否则该晶片为劣质品.
,则称该晶片为合格品,否则该晶片为劣质品.

(1)试求本次生产过程中该公司生产出合格品的频率以及数量;
(2)求这批晶片测试指标的平均值;
(3)现按照分层抽样的方法在测试指标在![]() 与
与![]() 之间的晶片中抽取6个晶片,再从这6个晶片中任取2个晶片进入深入分析,求恰有1个晶片的测试指标在
之间的晶片中抽取6个晶片,再从这6个晶片中任取2个晶片进入深入分析,求恰有1个晶片的测试指标在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com