
【题目】设函数![]() ,
,![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)讨论![]() 的单调性;
的单调性;
(2)证明:当![]() 时,
时,![]() ;
;
(3)确定![]() 的所有可能取值,使得
的所有可能取值,使得![]() 在
在![]() 区间内恒成立.
区间内恒成立.
【答案】(1)当![]()
![]() 时
时![]() 单调递减;当
单调递减;当![]()
![]() 时,
时,![]() 单调递增;
单调递增;
(2)详见解析;(3)![]()
![]() .
.
【解析】
试题分析:(1)首先对![]() 求导,然后对
求导,然后对![]() 进行讨论,从而判断函数的单调性;(2)利用导数判断函数的单调性,从而证明结论;(3)构造函数
进行讨论,从而判断函数的单调性;(2)利用导数判断函数的单调性,从而证明结论;(3)构造函数![]() (
(![]() ),利用导数判断函数
),利用导数判断函数![]() 的单调性,从而求解
的单调性,从而求解![]() 的值.
的值.
试题解析:(1)由![]() ,得
,得![]() .
.
当![]() 时,
时,![]() 在
在![]() 成立,则
成立,则![]() 为
为![]() 上的减函数;
上的减函数;
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
则![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数.
上为增函数.
综上,当![]() 时,
时,![]() 为
为![]() 上的减函数;当
上的减函数;当![]() 时,
时,![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数.
上为增函数.
(2)证明:要证![]() ,即
,即![]() ,即证
,即证![]() ,也就是证
,也就是证![]() .
.
令![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
,
即当![]() 时,
时,![]() ,∴当
,∴当![]() 时,
时,![]() ;
;
(3)由![]() ,得
,得![]() .
.
设![]() ,由题意知,
,由题意知,![]() 在
在![]() 内恒成立.
内恒成立.
∵![]() ,∴有
,∴有![]() 在
在![]() 内恒成立.
内恒成立.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,
令![]() ,
,![]() ,函数在
,函数在![]() 上单调递增.∴
上单调递增.∴![]() .
.
又![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
综上所述,![]() ,
,![]() ,
,![]() 在区间
在区间![]() 单调递增,
单调递增,
∴![]() ,即
,即![]() 在区间
在区间![]() 单调递增,∴
单调递增,∴![]() .
.


科目:高中数学 来源: 题型:
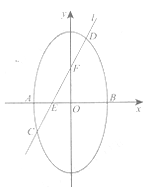
【题目】椭圆![]() 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线![]() 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线AD,CB的斜率分别为![]() ,若
,若![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
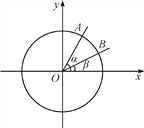
【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]() ,
,![]() .求:
.求:
(1)tan(α+β)的值;
(2)α+2β的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x+y)=f(x)+f(y),当x>0时,有![]() ,且f(1)=﹣2
,且f(1)=﹣2
(1)求f(0)及f(﹣1)的值;
(2)判断函数f(x)的单调性,并利用定义加以证明;
(3)求解不等式f(2x)﹣f(x2+3x)<4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() .
.
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤.
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
查看答案和解析>>
科目:高中数学 来源: 题型:
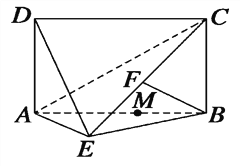
【题目】如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,
BF⊥平面ACE,且点F在CE上.
(1)求证:AE⊥BE;
(2)求三棱锥D—AEC的体积;
(3)设点M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,
使得MN∥平面DAE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 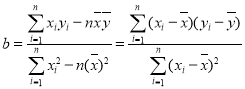 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com