解:(1)当n≥2时,
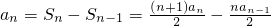
,(2分)
即
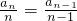
(n≥2).(4分)
所以数列

是首项为
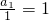
的常数列.(5分)
所以

,即a
n=n(n∈N
*).
所以数列{a
n}的通项公式为a
n=n(n∈N
*).(7分)
(2)假设存在k(k≥2,m,k∈N
*),使得b
k、b
k+1、b
k+2成等比数列,
则b
kb
k+2=b
k+12.(8分)
因为b
n=lna
n=lnn(n≥2),
所以
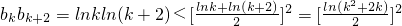
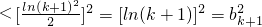
.(13分)
这与b
kb
k+2=b
k+12矛盾.
故不存在k(k≥2,k∈N
*),使得b
k、b
k+1、b
k+2成等比数列.(14分)
分析:(1)直接利用a
n=S
n-S
n-1 (n≥2)求解数列的通项公式即可(注意要验证n=1时通项是否成立).
(2)先利用(1)的结论求出数列{b
n}的通项,再求出b
kb
k+2的表达式,利用基本不等式得出不存在k(k≥2,k∈N
*),使得b
k、b
k+1、b
k+2成等比数列.
点评:本题考查了已知前n项和为S
n求数列{a
n}的通项公式,根据a
n和S
n的关系:a
n=S
n-S
n-1 (n≥2)求解数列的通项公式.另外,须注意公式成立的前提是n≥2,所以要验证n=1时通项是否成立,若成立则:a
n=S
n-S
n-1 (n≥1);若不成立,则通项公式为分段函数.

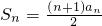 ,且a1=1.
,且a1=1.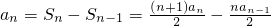 ,(2分)
,(2分)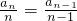 (n≥2).(4分)
(n≥2).(4分) 是首项为
是首项为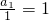 的常数列.(5分)
的常数列.(5分) ,即an=n(n∈N*).
,即an=n(n∈N*).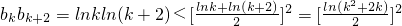
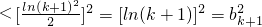 .(13分)
.(13分)
