

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源:不详 题型:解答题
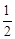 ,从陆路每个方向抵达灾区的概率都是
,从陆路每个方向抵达灾区的概率都是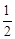 ,从空中抵达灾区的概率是
,从空中抵达灾区的概率是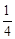 .
.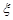 的数学期望.
的数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 男 | | 5 | |
| 女 | 10 | | |
| 合计 | | | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 其中
其中
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 (
( ≥0)万元,投资B项目资金为
≥0)万元,投资B项目资金为 (
( ≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利
≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利 的可能性为
的可能性为 ,亏损
,亏损 的可能性为
的可能性为 ;位于二类风区的B项目获利
;位于二类风区的B项目获利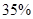 的可能性为
的可能性为 ,亏损
,亏损 的可能性是
的可能性是 ,不赔不赚的可能性是
,不赔不赚的可能性是 .
. 和
和 ,试写出随机变量
,试写出随机变量 与
与 的分布列和期望
的分布列和期望 ,
, ;
; 万元的资金投资于A,B项目,且公司要求对A项目的投
万元的资金投资于A,B项目,且公司要求对A项目的投 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,得到乙、丙两公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记X为该毕业生得到面试的公司个数.若P(X=0)=
,得到乙、丙两公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记X为该毕业生得到面试的公司个数.若P(X=0)= ,则随机变量X的数学期望E(X)=________.
,则随机变量X的数学期望E(X)=________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
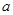 个红球,
个红球,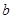 个黄球,
个黄球,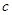 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,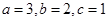 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求 分布列;
分布列; 为取出此球所得分数.若
为取出此球所得分数.若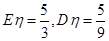 ,求
,求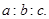
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com