
【题目】在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( ) 
A.31.2
B.32.4
C.33.6
D.34.8
【答案】B
【解析】解:由题意可得:BD=6,AB=12,AE=9,设∠BAD=α,则∠AEB=2α, ∵在△ABE中,由正弦定理可得: ![]() ,可得:sinB=
,可得:sinB= ![]() sin2α,
sin2α,
在△ABD中,由正弦定理可得: ![]() ,可得:AD=
,可得:AD= ![]() =9cosα,
=9cosα,
∴由余弦定理可得:62=122+(9cosα)2﹣2×12×(9cosα)×cosα,
整理可得:cosα= ![]() ,
,
∴sinα= ![]() ,sin2α=
,sin2α= ![]() ,cos2α=
,cos2α= ![]() ,AD=
,AD= ![]() ,
,
则在△ADE中,由余弦定理可得:( ![]() )2=DE2+92﹣2×9×DE×
)2=DE2+92﹣2×9×DE× ![]() ,整理可得:5DE2﹣54DE+81=0,
,整理可得:5DE2﹣54DE+81=0,
∴解得:DE=9,或1.8(舍去),
∴S△ADE= ![]() AEDEsin2α=
AEDEsin2α= ![]() ×9×9×
×9×9× ![]() =32.4.
=32.4.
故选:B.
【考点精析】本题主要考查了正弦定理的定义的相关知识点,需要掌握正弦定理:![]() 才能正确解答此题.
才能正确解答此题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
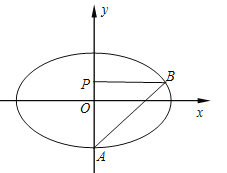
【题目】如图,点![]() 是椭圆
是椭圆![]() :
:![]() 的短轴位于
的短轴位于![]() 轴下方的端点,过
轴下方的端点,过![]() 作斜率为1的直线交椭圆于
作斜率为1的直线交椭圆于![]() 点,点
点,点![]() 在
在![]() 轴上,且
轴上,且![]() 轴,
轴, ![]() .
.
(1)若点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)若点![]() 的坐标为
的坐标为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有 2个红球和 2个白球的口袋中任取 2个球,则下列每对事件中,互斥事件的对数是( )对
(1)“至少有 1个白球”与“都是白球” (2)“至少有 1个白球”与“至少有 1个红球”
(3)“至少有 1个白球”与“恰有 2个白球” (4)“至少有 1个白球”与“都是红球”
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的公差d>0,前n项和为Sn , 已知3 ![]() 是﹣a2与a9的等比中项,S10=﹣20.
是﹣a2与a9的等比中项,S10=﹣20.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn(n≥6).
,求数列{bn}的前n项和Tn(n≥6).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一动圆与圆![]() 外切,与圆
外切,与圆![]() 内切.
内切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)设过圆心![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,
两点,![]() (
(![]() 为圆
为圆![]() 的圆心)的内切圆
的圆心)的内切圆![]() 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com