设等比数列{an}的首项为a,公比q>0且q≠1,前n项和为Sn.
(Ⅰ)当a=1时,S1+1,S2+2,S3+1三数成等差数列,求数列{an}的通项公式;
(Ⅱ)对任意正整数n,命题甲:Sn,(Sn+1+1),Sn+2三数构成等差数列. 命题乙:Sn+1,(Sn+2+1),Sn+3三数构成等差数列.求证:对于同一个正整数n,命题甲与命题乙不能同时为真命题.
解:(Ⅰ)∵数列{a
n}是首项为a=1,公比q>0且q≠1的等比数列,
∴
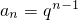
,∴S
1+1=1+1=2,S
2+2=1+q+2=q+3,S
3+1=1+q+q
2+1=2+q+q
2,
又∵S
1+1,S
2+2,S
3+1三数成等差数列,∴2(S
2+2)=(S
1+1)+(S
3+1),∴2(q+3)=2+2+q+q
2,化为q
2-q-2=0,
解得q=2,或q=-1,
∵q>0,∴q=2,∴
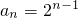
.
所以数列{a
n}的通项公式为
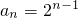
.
(Ⅱ)对任意正整数n,命题甲:S
n,(S
n+1+1),S
n+2三数构成等差数列,?2(S
n+1+1)=S
n+S
n+2?a
n+2=a
n+1+2;
对任意正整数n,命题乙:S
n+1,(S
n+2+1),S
n+3三数构成等差数列,?2(S
n+2+1)=S
n+1+S
n+3?a
n+3=a
n+2+2
若对于同一个正整数n,命题甲与命题乙同时为真命题,则a
n+3-a
n+2=a
n+2-a
n+1.
∴
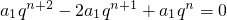
,又
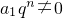
,
∴q
2-2q+1=0,∴q=1与已知q≠1相矛盾.
所以对于同一个正整数n,命题甲与命题乙不能同时为真命题.
分析:(Ⅰ)由已知条件S
1+1,S
2+2,S
3+1三数成等差数列,∴2(S
2+2)=(S
1+1)+(S
3+1),再由通项公式及前n项和公式及a=1,可求出q的值.
(Ⅱ)先假设对于同一个正整数n,命题甲与命题乙同时为真命题,由此可得出q=1,从而得出矛盾.
点评:本题综合考查了等差数列与等比数列的通项公式及前n项和公式,熟练掌握以上有关知识是解决问题的关键.

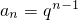 ,∴S1+1=1+1=2,S2+2=1+q+2=q+3,S3+1=1+q+q2+1=2+q+q2,
,∴S1+1=1+1=2,S2+2=1+q+2=q+3,S3+1=1+q+q2+1=2+q+q2,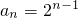 .
.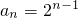 .
.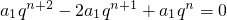 ,又
,又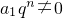 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案