
设函数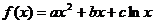 ,(其中
,(其中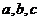 为实常数且
为实常数且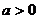 ),曲线
),曲线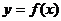 在点
在点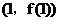 处的切线方程为
处的切线方程为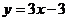 .
.
(Ⅰ) 若函数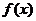 无极值点且
无极值点且 存在零点,求
存在零点,求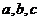 的值;
的值;
(Ⅱ) 若函数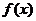 有两个极值点,证明
有两个极值点,证明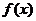 的极小值小于
的极小值小于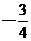 .
.
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
| 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年温州八校适应性考试三理) (16分) 已知函数![]() ,其中
,其中![]() 为实常数,设
为实常数,设![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当![]() 时,求
时,求![]() 的极值;
的极值;
(Ⅱ)若![]() 在区间
在区间![]() 上的最大值为-3,求
上的最大值为-3,求![]() 的值;
的值;
(III)当![]() 时,试推断方程
时,试推断方程 ![]() 是否有实数解.
是否有实数解.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省宁波市鄞州区高三高考适应性3月考试理科数学 题型:解答题
(本小题满分15分)设函数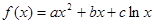 ,(其中
,(其中 为实常数且
为实常数且 ),曲线
),曲线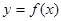 在点
在点 处的切线方程为
处的切线方程为 .
.
(Ⅰ)
若函数 无极值点且
无极值点且 存在零点,求
存在零点,求 的值;
的值;
(Ⅱ) 若函数 有两个极值点,证明
有两个极值点,证明 的极小值小于
的极小值小于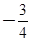 .
.
查看答案和解析>>
科目:高中数学 来源:2014届吉林省高一下学期期初考试数学试卷(解析版) 题型:解答题
P(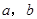 )是平面上的一个点,设事件A表示“
)是平面上的一个点,设事件A表示“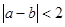 ”,其中
”,其中 为实常数.
为实常数.
(1)若 均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
(2)若 均为从区间[0,5)任取的一个数,求事件A发生的概率.
均为从区间[0,5)任取的一个数,求事件A发生的概率.
【解析】本试题考查了几何概型和古典概型结合的一道综合概率计算试题。首先明确区域中的所有基本事件数或者区域表示的面积,然后分别结合概率公式求解得到。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com