
已知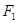 、
、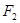 分别为椭圆
分别为椭圆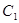 :
: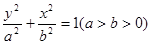 的上、下焦点,其中
的上、下焦点,其中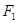 也是抛物线
也是抛物线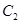 :
: 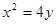 的焦点,点
的焦点,点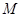 是
是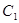 与
与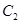 在第二象限的交点,且
在第二象限的交点,且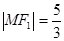 。
。
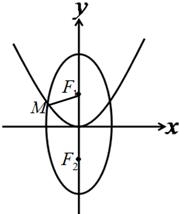
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点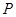 (1,3)和圆
(1,3)和圆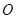 :
: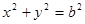 ,过点
,过点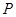 的动直线
的动直线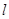 与圆
与圆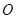 相交于不同的两点
相交于不同的两点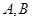 ,在线段
,在线段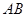 取一点
取一点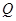 ,满足:
,满足: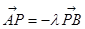 ,
,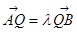 (
(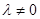 且
且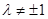 )。
)。
求证:点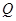 总在某定直线上。
总在某定直线上。
(Ⅰ)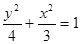 (Ⅱ)设
(Ⅱ)设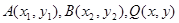 由
由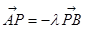 可得
可得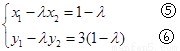 由
由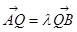 可得
可得 ⑤×⑦得:
⑤×⑦得: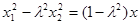 ,⑥×⑧得:
,⑥×⑧得: ,两式相加得
,两式相加得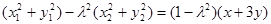 又点A,B在圆
又点A,B在圆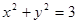 上,且
上,且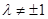 ,
,
所以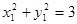 ,
,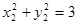 即
即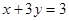 ,所以点Q总在定直线
,所以点Q总在定直线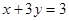 上
上
【解析】
试题分析:(1)由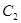 :
: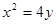 知
知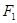 (0,1),设
(0,1),设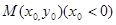 ,因M在抛物线
,因M在抛物线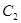 上,故
上,故
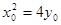 ① 又
① 又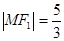 ,则
,则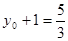 ②,
②,
由①②解得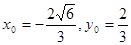 (3分)
(3分)
椭圆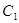 的两个焦点
的两个焦点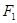 (0,1),
(0,1),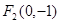 ,点M在椭圆上,有椭圆定义可得
,点M在椭圆上,有椭圆定义可得
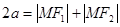
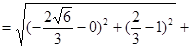
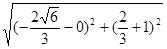
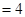
∴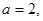 又
又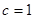 ,∴
,∴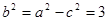 ,椭圆
,椭圆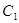 的方程为:
的方程为: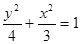 (6分)
(6分)
(2)设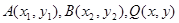 ,
,
由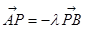 可得:
可得: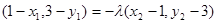 ,
,
即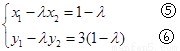 (9分)
(9分)
由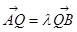 可得:
可得: ,
,
即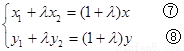
⑤×⑦得: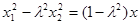
⑥×⑧得: (10分)
(10分)
两式相加得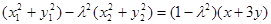 (11分)
(11分)
又点A,B在圆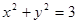 上,且
上,且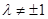 ,
,
所以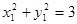 ,
,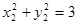
即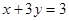 ,所以点Q总在定直线
,所以点Q总在定直线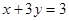 上 (12分)
上 (12分)
考点:椭圆抛物线方程性质及直线与圆相交
点评:解题时充分利用抛物线的定义:抛物线上的点到焦点的距离等于到准线的距离,能使解题过程简化;第二问中的向量关系常转化为点的坐标关系,证明点在定直线上的主要思路是验证点的坐标始终满足于某直线方程


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| BF1 |
| BF2 |
| 1 |
| 2 |
| F1F22 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
查看答案和解析>>
科目:高中数学 来源:2014届广东深圳第二高级中学高三上学期第一次月考文科数学试卷(解析版) 题型:选择题
已知 、
、 分别为椭圆
分别为椭圆 的两个焦点,点
的两个焦点,点 为其短轴的一个端点,若
为其短轴的一个端点,若 为等边三角形,则该椭圆的离心率为(
)
为等边三角形,则该椭圆的离心率为(
)
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三下学期3月联考理科数学 题型:解答题
(本小题满分15分).
已知 、
、 分别为椭圆
分别为椭圆 :
: 的
的
上、下焦点,其中 也是抛物线
也是抛物线 :
: 的焦点,
的焦点,
点 是
是 与
与 在第二象限的交点,且
在第二象限的交点,且 。
。
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点P(1,3)和圆 :
: ,过点P的动直线
,过点P的动直线 与圆
与圆 相交于不同的两点A,B,在线段AB取一点Q,满足:
相交于不同的两点A,B,在线段AB取一点Q,满足: ,
, (
( 且
且 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。

查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三12月月考文科数学试卷 题型:选择题
已知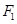 、
、 分别为椭圆C:
分别为椭圆C: 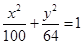 的左、右焦点,点A∈C且
的左、右焦点,点A∈C且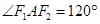 ,则
,则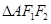 的面积为( )
的面积为( )
A.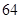 B.
B.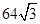 C.
C.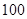 D.
D.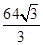
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com