
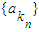 中的前n项的积为数列
中的前n项的积为数列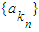 的n项阶乘,记为
的n项阶乘,记为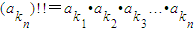 ,例如:(a3n+1)!!=a4•a7•a10•…•a3n+1,已知f(x)=x-sinx在[0,n]上的最大值为bn;设an=bn+sin n.
,例如:(a3n+1)!!=a4•a7•a10•…•a3n+1,已知f(x)=x-sinx在[0,n]上的最大值为bn;设an=bn+sin n.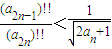
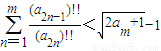 成立?若存在,求出所有的m的值;若不存在,请说明理由.
成立?若存在,求出所有的m的值;若不存在,请说明理由.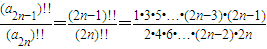 和
和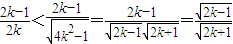 能够证明
能够证明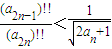 .
.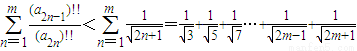 =
=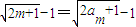 ,知对于任意的m∈N*均有
,知对于任意的m∈N*均有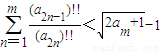 .
.
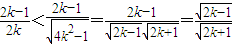 ,
, ,
,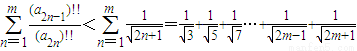
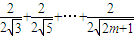
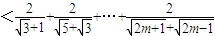

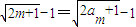 ,
,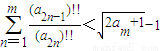 .
.

科目:高中数学 来源: 题型:解答题
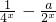 (a∈R)
(a∈R)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省广州市东风中学高三数学综合训练试卷8(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2007年上海市徐汇区零陵中学高三3月综合练习数学试卷(一)(解析版) 题型:解答题
 +
+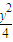 =1,直线l的方程是y=x+3.
=1,直线l的方程是y=x+3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com