
【题目】若函数![]() 在
在![]() 处有极大值,则常数
处有极大值,则常数![]() 为( )
为( )
A. 2或6 B. 2 C. 6 D. ![]() 或
或![]()
【答案】C
【解析】分析:求出函数的导数,再令导数等于0,求出c 值,再检验函数的导数是否满足在x=2处左侧为正数,右侧为负数,把不满足条件的 c值舍去.
详解:∵函数f(x)=x(x﹣c)2=x3﹣2cx2+c2x,它的导数为![]() =3x2﹣4cx+c2,
=3x2﹣4cx+c2,
由题意知在x=2处的导数值为 12﹣8c+c2=0,∴c=6或 c=2,
又函数f(x)=x(x﹣c)2在x=2处有极大值,
故导数值在x=2处左侧为正数,右侧为负数.
当c=2时,![]() =3x2﹣8x+4=3(x﹣
=3x2﹣8x+4=3(x﹣![]() )(x﹣2),
)(x﹣2),
不满足导数值在x=2处左侧为正数,右侧为负数.
当c=6时,![]() =3x2﹣24x+36=3(x2﹣8x+12)=3(x﹣2)(x﹣6),
=3x2﹣24x+36=3(x2﹣8x+12)=3(x﹣2)(x﹣6),
满足导数值在x=2处左侧为正数,右侧为负数.故 c=6.
故答案为:C


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知长方形ABCD,AD=2CD=4,M、N分别为AD、BC的中点,将长方形ABCD沿MN折到MNFE位置,且使平面MNFE⊥平面ABCD.
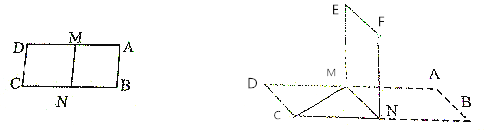
(1)求证:直线CM⊥面DFN;
(2)求点C到平面FDM的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 是直线
是直线![]() 上的动点,定点
上的动点,定点![]() 点
点![]() 为
为![]() 的中点,动点
的中点,动点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程
的方程
(2)过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() 两点,
两点,![]() 为
为![]() 上任意一点,直线
上任意一点,直线![]() 交
交![]() 于
于![]() 两点,以
两点,以![]() 为直径的圆是否过
为直径的圆是否过![]() 轴上的定点? 若过定点,求出定点的坐标;若不过定点,说明理由。
轴上的定点? 若过定点,求出定点的坐标;若不过定点,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() 为抛物线
为抛物线![]() 上不同的四点,且点
上不同的四点,且点![]() 关于
关于![]() 轴对称,
轴对称,![]() 平行于该抛物线在点
平行于该抛物线在点![]() 处的切线
处的切线![]() .
.
(1)求证:直线![]() 与直线
与直线![]() 的倾斜角互补;
的倾斜角互补;
(2)若![]() ,且
,且![]() 的面积为16,求直线
的面积为16,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业2017年的纯利润为500万元,因设备老化等原因,企业的生产能力逐年下降,若不能进行技术改造,预测从2018年起每年比上一年纯利润减少20万元,2018年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第![]() 年(以2018年为第一年)的利润为
年(以2018年为第一年)的利润为![]() 万元(
万元(![]() 为正整数).
为正整数).
(1)设从今年起的前![]() 年,若该企业不进行技术改造的累计纯利润为
年,若该企业不进行技术改造的累计纯利润为![]() 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为![]() 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求![]() ,
,![]() 的表达式;
的表达式;
(2)依上述预测,从2018年起该企业至少经过多少年,进行技术改造后的累计利润超过不进行技术改造的累计纯利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a为实数,函数f(x)=x2﹣|x2﹣ax﹣2|在区间(﹣∞,﹣1)和(2,+∞)上单调递增,则a的取值范围为( )
A.[1,8]
B.[3,8]
C.[1,3]
D.[﹣1,8]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com