Question

9．如图，在矩形 OABC中，$\overrightarrow{{A}{B}}=3\overrightarrow{{A}{E}}$，$\overrightarrow{{B}C}=3\overrightarrow{FC}$，若$\overrightarrow{{O}{B}}=λ\overrightarrow{{O}{E}}+μ\overrightarrow{{O}F}$（λ，μ∈R），则λμ等于（　　）

• A． $\frac{9}{4}$
• B． $\frac{9}{16}$
• C． $\frac{4}{9}$
• D． $\frac{16}{9}$

Answer 1

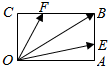
分析 $\overrightarrow{OB}$=$\overrightarrow{OA}$+$\overrightarrow{AB}$，然后用$\overrightarrow{OA}$，$\overrightarrow{AB}$表示出$\overrightarrow{OE}$，$\overrightarrow{OF}$，得到λ，μ的值．

解答 解：∵$\overrightarrow{{A}{B}}=3\overrightarrow{{A}{E}}$，$\overrightarrow{{B}C}=3\overrightarrow{FC}$，
∴$\overrightarrow{OE}$=$\overrightarrow{OA}$+$\overrightarrow{AE}$=$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{AB}$，$\overrightarrow{OF}$=$\overrightarrow{OC}$+$\overrightarrow{CF}$=$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{BC}$=$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{OA}$，
∴$\overrightarrow{{O}{B}}=λ\overrightarrow{{O}{E}}+μ\overrightarrow{{O}F}$=λ（$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{AB}$）+μ（$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{OA}$）=（$λ+\frac{μ}{3}$）$\overrightarrow{OA}$+（$\frac{λ}{3}+μ$）$\overrightarrow{AB}$．
又∵$\overrightarrow{OB}$=$\overrightarrow{OA}$+$\overrightarrow{AB}$，
∴$λ+\frac{μ}{3}$=$\frac{λ}{3}+μ$=1，解得λ=μ=$\frac{3}{4}$，
∴λμ=$\frac{9}{16}$．
故选：B．

点评 本题考查了平面向量加法的几何意义，属于基础题．