
【题目】已知向量![]() ,
,![]() ,
,![]() ,函数
,函数![]() .
.
(1)求函数![]() 的对称中心;
的对称中心;
(2)设锐角![]() 三个内角
三个内角![]() 所对的边分别为
所对的边分别为![]() ,若
,若![]() 求
求![]() 和c
和c
科目:高中数学 来源: 题型:
【题目】某服务电话,打进的电话响第1声时被接的概率是0.1;响第2声时被接的概率是0.2;响第3声时被接的概率是0.3;响第4声时被接的概率是0.35.
(1)打进的电话在响5声之前被接的概率是多少?
(2)打进的电话响4声而不被接的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 与双曲线
与双曲线 ![]() 的离心率相同,且双曲线C2的左、右焦点分别为F1 , F2 , M是双曲线C2一条渐近线上的某一点,且OM⊥MF2 ,
的离心率相同,且双曲线C2的左、右焦点分别为F1 , F2 , M是双曲线C2一条渐近线上的某一点,且OM⊥MF2 , ![]() ,则双曲线C2的实轴长为( )
,则双曲线C2的实轴长为( )
A.4
B.![]()
C.8
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
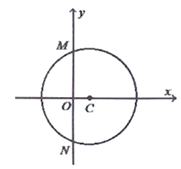
【题目】已知圆心在x轴正半轴上的圆C与直线![]() 相切,与y轴交于M,N两点,且
相切,与y轴交于M,N两点,且![]() .
.
![]() Ⅰ
Ⅰ![]() 求圆C的标准方程;
求圆C的标准方程;
![]() Ⅱ
Ⅱ![]() 过点
过点![]() 的直线l与圆C交于不同的两点D,E,若
的直线l与圆C交于不同的两点D,E,若![]() 时,求直线l的方程;
时,求直线l的方程;
![]() Ⅲ
Ⅲ![]() 已知Q是圆C上任意一点,问:在x轴上是否存在两定点A,B,使得
已知Q是圆C上任意一点,问:在x轴上是否存在两定点A,B,使得![]() ?若存在,求出A,B两点的坐标;若不存在,请说明理由.
?若存在,求出A,B两点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个港口,相邻两次高潮发生时间相距![]() ,低潮时水的深度为
,低潮时水的深度为![]() ,高潮时为
,高潮时为![]() ,一次高潮发生在10月10日4:00,每天涨潮落潮时,水的深度
,一次高潮发生在10月10日4:00,每天涨潮落潮时,水的深度![]() 与时间
与时间![]() 近似满足关系式
近似满足关系式![]() .
.
(1)若从10月10日0:00开始计算时间,选用一个三角函数来近似描述该港口的水深![]() 和时间
和时间![]() 之间的函数关系.
之间的函数关系.
(2)10月10日17:00该港口水深约为多少?(精确到![]() )
)
(3)10月10日这一天该港口共有多长时间水深低于![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值m | m<185 | 185≤m<205 | m≥205 |
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图: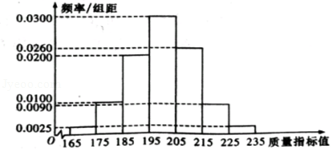
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(Ⅱ)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(III)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(218,140}),则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为落实国家“精准扶贫”政策,让市民吃上放心蔬菜,某企业于2017年在其扶贫基地投入100万元研发资金,用于蔬菜的种植及开发,并计划今后十年内在此基础上,每年投入的资金比上一年增长![]() .
.
(1)写出第![]() 年(2018年为第一年)该企业投入的资金数
年(2018年为第一年)该企业投入的资金数![]() (万元)与
(万元)与![]() 的函数关系式,并指出函数的定义域
的函数关系式,并指出函数的定义域
(2)该企业从第几年开始(2018年为第一年),每年投入的资金数将超过200万元?(参考数据![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com