
给出下列四个命题:
(1)方程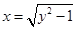 表示双曲线的一部分;
表示双曲线的一部分;
(2)动点到两个定点的距离之和为定长,则动点的轨迹为椭圆;
(3)动点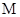 与点
与点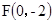 的距离比它到直线
的距离比它到直线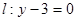 的距离小1的轨迹方程是
的距离小1的轨迹方程是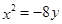 ;
;
(4)若双曲线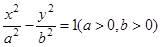 的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点
的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点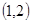 在“上”区域内,则双曲线的离心率
在“上”区域内,则双曲线的离心率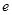 的取值范围是
的取值范围是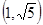 .其中所有正确命题的序号是 .
.其中所有正确命题的序号是 .
(1)(3)(4)
【解析】
试题分析:对于命题1,由于方程两边平方得到为双曲线的方程,因此可知表示的为双曲线的一部分,因此正确,命题2,当定值为两定点的距离时,轨迹不是椭圆而是一条线段,因此错误,
命题3,动点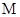 与点
与点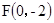 的距离比它到直线
的距离比它到直线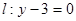 的距离小1的轨迹方程转化为动点
的距离小1的轨迹方程转化为动点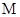 与点
与点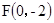 的距离比它到直线y=2的距离相等,因此可知其方程为
的距离比它到直线y=2的距离相等,因此可知其方程为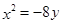 ;正确。
;正确。
命题4,若双曲线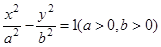 的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点
的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点 在“上”区域内,则说明了渐近线 斜率小于2,则可知双曲线的离心率
在“上”区域内,则说明了渐近线 斜率小于2,则可知双曲线的离心率 的取值范围是
的取值范围是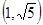 ,故正确的序号为(1)(3)(4)。
,故正确的序号为(1)(3)(4)。
考点:本试题考查了轨迹方程的知识。
点评:解决该是的关键是理解圆锥曲线的定义,同时要准确的理解定义,以及其性质与方程之间的关系,对于轨迹方程的求解,一般先考虑运用定义法,然后考虑别的求解方法,属于中档题。


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| y-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 12 |
| π |
| 12 |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2x-1 |
| (1+2x)2 |
| x•2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com