
【题目】若x,y满足约束条件 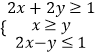 ,且向量
,且向量 ![]() =(3,2),
=(3,2), ![]() =(x,y),则
=(x,y),则 ![]()
![]() 的取值范围( )
的取值范围( )
A.[ ![]() ,5]
,5]
B.[ ![]() ,5]
,5]
C.[ ![]() ,4]
,4]
D.[ ![]() ,4]
,4]
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C= ![]() . (Ⅰ)若△ABC的面积等于
. (Ⅰ)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(Ⅱ)若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C为△ABC的三个内角,且其对边分别为a,b,c,若c2+b2+cb=a2
(1)求A;
(2)若a=2 ![]() ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC. 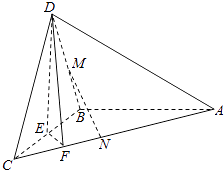
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN= ![]() CA,求证:MN∥平面DEF.
CA,求证:MN∥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点. 
(1)求线段AP中点的轨迹方程;
(2)若∠PBQ=90°,求线段PQ中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等差数列{an},满足|a10a11|>a10a11 , 且a102<a112 , Sn为其前n项和,则( )
A.a8+a12>0
B.S1 , S2 , …S19都小于零,S10为Sn的最小值
C.a8+a13<0
D.S1 , S2 , …S20都小于零,S10为Sn的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com