
分析 (1)可考虑去绝对值,对f(x)=|ax+b|两边平方得到,f2(x)=a2x2+2abx+b2,可设g(x)=f2(x),g(x)便是二次函数,从而可讨论对称轴和区间[-1,1]的关系:分成$-\frac{b}{a}≤-1$,$-1<-\frac{b}{a}≤0$,$0<-\frac{b}{a}<1$,和$-\frac{b}{a}≥1$四种情况,然后根据g(x)在[-1,1]的单调性或通过比较端点值的大小,从而求出g(x)的最大值,进而便可求出f(x)的最大值D=$\left\{\begin{array}{l}{|a+b|}&{-\frac{b}{a}≤0}\\{|a-b|}&{-\frac{b}{a}>0}\end{array}\right.$;
(2)根据求得的最大值D的表达式,在该分段函数的每一段里,找出满足D≤1的点(a,b)所在的平面区域,然后求出平面区域的面积即可.
解答 解:(1)f2(x)=a2x2+2abx+b2,设g(x)=a2x2+2abx+b2,a2>0,该函数的对称轴为x=$-\frac{b}{a}$;
①若$-\frac{b}{a}≤-1$,则g(x)在[-1,1]上单调递增;
∴g(x)的最大值为g(1)=(a+b)2;
∴f(x)的最大值D=|a+b|;
②若$-1<-\frac{b}{a}≤0$,g(-1)=(a-b)2≤(a+b)2;
∴g(x)的最大值为(a+b)2;
∴f(x)的最大值D=|a+b|;
③若$0<-\frac{b}{a}<1$,则g(-1)>g(1);
∴g(x)的最大值为(a-b)2;
∴f(x)的最大值D=|a-b|;
④若$-\frac{b}{a}≥1$,则g(x)在[-1,1]上单调递减;
∴g(x)的最大值为g(-1)=(a-b)2;
∴f(x)的最大值D=|a-b|;
∴$D=\left\{\begin{array}{l}{|a+b|}&{-\frac{b}{a}≤0}\\{|a-b|}&{-\frac{b}{a}>0}\end{array}\right.$;
(2)根据上面求得的D:
①$-\frac{b}{a}≤0$时,D=|a+b|;
a>0时,b≥0,a<0时,b≤0;
又|a+b|≤1;
即-1≤a+b≤1;
所以不等式组$\left\{\begin{array}{l}{-\frac{b}{a}≤0}\\{-1≤a+b≤1}\end{array}\right.$表示的平面区域,如下图阴影部分所示: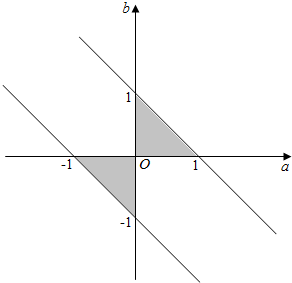
∴点(a,b)所在平面区域的面积S=1;
②$-\frac{b}{a}>0$时,D=|a-b|;
a>0时,b<0,a<0时,b>0,且|a-b|≤1;
即-1≤a-b≤1;
∴不等式组$\left\{\begin{array}{l}{-\frac{b}{a}>0}\\{-1≤a-b≤1}\end{array}\right.$表示的平面区域如下图阴影部分所示: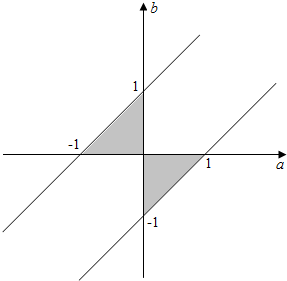
∴点(a,b)所在平面区域的面积S=1.
点评 考查含绝对值函数的处理方法:函数解析式两边平方,二次函数的对称轴,二次函数的单调性,以及根据单调性定义或比较端点值求二次函数在闭区间上的最大值的方法,能找出不等式组所表示的平面区域.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
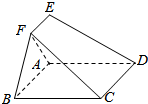 在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )
在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
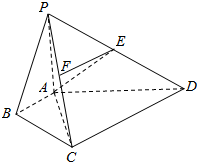 在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.
在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {3} | C. | {1,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [1,2] | C. | [10,100] | D. | [0,lg2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
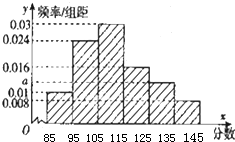 某市在2 015年2月份的高三期末考试中对数学成绩数据统计显示,全市10000名学生的成绩服从正态分布N (120,25),现某校随机抽取了50名学生的数学成绩分析,结果这50名同学的成绩全部介于80分到140分之间现将结果按如下方式分为6组,第一组[85,95),第二组[95,105),…第六组[135,145],得到如图所示的频率分布直方图.
某市在2 015年2月份的高三期末考试中对数学成绩数据统计显示,全市10000名学生的成绩服从正态分布N (120,25),现某校随机抽取了50名学生的数学成绩分析,结果这50名同学的成绩全部介于80分到140分之间现将结果按如下方式分为6组,第一组[85,95),第二组[95,105),…第六组[135,145],得到如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com