Question

已知函数f（x）=bx，g（x）=ax²+1，h（x）=lnx．（a，b∈R）
（1）若M={x|f（x）+g（x）≥0}，-1∈M，2∈M，z=3a-b，求z的取值范围；
（2）设F(x)=

h(x)

f(x)

，且b＜0，试判断函数F（x）的单调性；
（3）试证明：对?n∈N^*，不等式ln(

1+n

n

)e＜

1+n

n

恒成立．

Answer 1

分析：（1）解法一：由f（x）+g（x）≥0，}，-1∈M，2∈M，我们易得

a-b+1≥0 4a+2b+1≥0

，然后利用线性规划，求出目标函数z=3a-b的取值范围；
解法二：令h（x）=f（x）+g（x）由-1∈M，2∈M得h（-1）≥0，h（2）≥0，分别用h（-1），h（2）表示a，b，进而根据不等式的性质，得到z的取值范围；
（2）由已知中F(x)=

h(x)

f(x)

，且b＜0，我们可以分别求出函数F（x）的解析式及其导函数的解析式，然后利用导数学判断出函数F（x）的单调性；
（3）证法一：由（2）中结论，可得在（0，+∞）上恒有F(x)=

lnx

bx

≥

1

be

，即

lnx

x

≤

1

e

，进而根据对数的运算性质证得答案．
证法二：构造函数p(x)=lnx-

x

e

，x∈（0，+∞），利用导数法，可以证得p（x）在（0，e]上单调递增，在[e，+∞）上单调递减，即对任意的x∈（0，+∞）恒有lnx-

1

e

x≤0，即lnx≤

1

e

x进而根据对数的运算性质证得答案．

解答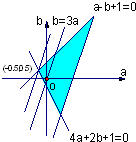：解：（1）解法1：不等式f（x）+g（x）≥0即ax²+bx+1≥0
由-1∈M，2∈M得

a-b+1≥0 4a+2b+1≥0

----------------（2分）
画出不等式组所确定的可行域如右图示：作平行线族b=3a-z
可见当a=-0.5，b=0.5时z有最小值，，z_min=-2
∴z的取值范围为z≥-2．----------------------------------------（4分）
解法2：令h（x）=f（x）+g（x）由-1∈M，2∈M得h（-1）≥0，h（2）≥0
由

a-b+1=h(-1) 4a+2b+1=h(2)

得

a= h(2)+2h(-1)-3 6 b= h(2)-4h(-1)+3 6

-------------------------（2分）
∴3a-b=

1

3

h(2)+

5

3

h(-1)-2
∵h（-1）≥0，h（2）≥0∴3a-b≥-2，即z的取值范围为z≥-2．------------（4分）]
（2）∵F(x)=

lnx

bx

∴F′(x)=

1-lnx

bx2

-----------------------------------（6分）
令F'（x）=0得1-lnx=0
∴x=e------------------------------------------------------------（7分）
∵当0＜x＜e时F′(x)=

1-lnx

bx2

＜0，当x＞e时F'（x）＞0
∴函数F（x）在（0，e]上单调递减，在[e，+∞）上单调递增--------------------------（9分）
（3）证法1：由（2）知当x=e时函数有最小值F(x)min=F(e)=

1

be

∴在（0，+∞）上恒有F(x)=

lnx

bx

≥

1

be

，------------------------------------------------（11分）
∵b＜0∴

lnx

x

≤

1

e

当且仅当x=e时“=”成立
∴对任意的x∈（0，+∞）恒有lnx≤

1

e

x--------------------------------------------------（12分）
∵

1+n

n

＞0且

1+n

n

≠e∴ln

1+n

n

＜

1

e

•

1+n

n

?ln(

1+n

n

)e＜

1+n

n

即对?n∈N^*，不等式ln(

1+n

n

)e＜

1+n

n

恒成立．-----------------------------------------（14分）
〔证法2：构造函数p(x)=lnx-

x

e

，x∈（0，+∞）----------------------------------------（10分）
令p′(x)=

1

x

-

1

e

=0得x=e
∵当0＜x＜e时p'（x）＞0，当x＞e时p'（x）＜0
∴函数p（x）在（0，e]上单调递增，在[e，+∞）上单调递减----------------------（12分）
当x=e时函数p（x）有最大值p（x）_max=p（e）=0
∴对任意的x∈（0，+∞）恒有lnx-

1

e

x≤0，即lnx≤

1

e

x
∵

1+n

n

＞0且

1+n

n

≠e∴ln

1+n

n

＜

1

e

•

1+n

n

?ln(

1+n

n

)e＜

1+n

n

即对?n∈N^*，不等式ln(

1+n

n

)e＜

1+n

n

恒成立．-----------------------------------------（14分）

点评：本题考查的知识点是简单线性规划，利用导数研究函数的单调性，利用导数求闭区间上函数的最值，是应用导数确定函数性质类问题中比较难的类型，而且还综合和对数的性质，不等式的证明等难点，属高难度题型．