
 ,
, .
. ;
;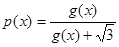 ,求证:
,求证: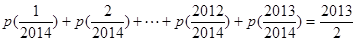 ;
; 是实数集
是实数集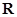 上的奇函数,且
上的奇函数,且 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数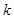 的取值范围.
的取值范围.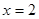 ;(2)参考解析;(3)
;(2)参考解析;(3)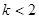
 ,
, ,所以解方程
,所以解方程 .通过换元即可转化为解二次方程.即可求得结论.
.通过换元即可转化为解二次方程.即可求得结论.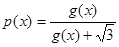 即得到
即得到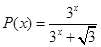 .所以
.所以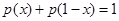 .所以两个一组的和为1,还剩中间一个
.所以两个一组的和为1,还剩中间一个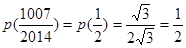 .即可求得结论.
.即可求得结论. 是实数集
是实数集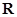 上的奇函数,可求得
上的奇函数,可求得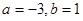 .又由于
.又由于 对任意实数
对任意实数 恒成立.该式的理解较困难,所以研究函数
恒成立.该式的理解较困难,所以研究函数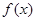 的单调性可得.函数
的单调性可得.函数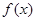 在实数集上是递增.集合奇函数,由函数值大小即可得到变量的大小,再利用基本不等式,从而得到结论.
在实数集上是递增.集合奇函数,由函数值大小即可得到变量的大小,再利用基本不等式,从而得到结论.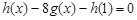 即:
即: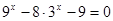 ,解得
,解得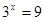 ,
,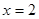
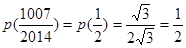 .
.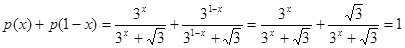 ,
,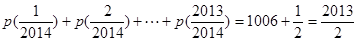 ,
,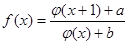 是实数集上的奇函数,所以
是实数集上的奇函数,所以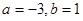 .
.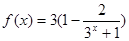 ,
,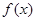 在实数集上单调递增.
在实数集上单调递增.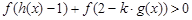 得
得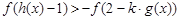 ,又因为
,又因为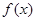 是实数集上的奇函数,所以,
是实数集上的奇函数,所以,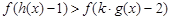 ,
,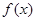 在实数集上单调递增,所以
在实数集上单调递增,所以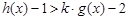
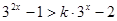 对任意的
对任意的 都成立,
都成立,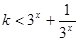 对任意的
对任意的 都成立,
都成立,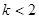 .
.

科目:高中数学 来源:不详 题型:解答题
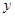 (万元)与处理量
(万元)与处理量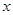 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: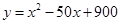 ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为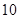 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴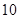 万元.
万元.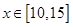 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的单位:s,v的单位:m/s)行驶至停止,在此期间汽车继续行驶的距离(单位:m)是( )
的单位:s,v的单位:m/s)行驶至停止,在此期间汽车继续行驶的距离(单位:m)是( )| A.1+25ln5 | B.8+25ln | C.4+25ln5 | D.4+50ln2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 立方米,且
立方米,且 . 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )
. 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )
A. | B.1 | C. | D.2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 上的函数
上的函数 ,如果存在函数
,如果存在函数 (
( 为常数),使得
为常数),使得 对一切实数
对一切实数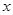 都成立,那么称
都成立,那么称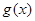 为函数
为函数 的一个承托函数.给出如下四个结论:
的一个承托函数.给出如下四个结论: ,其承托函数可能不存在,也可能有无数个;
,其承托函数可能不存在,也可能有无数个; 的函数
的函数 不存在承托函数;
不存在承托函数;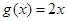 为函数
为函数 的一个承托函数;
的一个承托函数;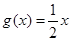 为函数
为函数 的一个承托函数.
的一个承托函数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com