
【题目】某百货公司1~6月份的销售量![]() 与利润
与利润![]() 的统计数据如下表:
的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
附:
(1)根据2~5月份的统计数据,求出![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]()
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过![]() 万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?(参考公式:,
万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?(参考公式:,![]() )
)
科目:高中数学 来源: 题型:
【题目】某学校有初级教师21人,中级教师14人,高级教师7人,现采用分层抽样的方法从这些教师中抽取6人对绩效工资情况进行调查.
(1)求应从初级教师,中级教师,高级教师中分别抽取的人数;
(2)若从抽取的6名教师中随机抽取2名做进一步数据分析,求抽取的2名均为初级教师的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() ,点
,点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() (不在y轴上).
(不在y轴上).

(1)若直线![]() 的斜率为3,求
的斜率为3,求![]() 的长度;
的长度;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值,并求出该定值;
为定值,并求出该定值;
(3)设![]() 的中点为
的中点为![]() ,是否存在直线
,是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() :
: ![]() 的上、下焦点,
的上、下焦点, ![]() 是抛物线
是抛物线![]() :
: ![]() 的焦点,点
的焦点,点![]() 是
是![]() 与
与![]() 在第二象限的交点,且
在第二象限的交点,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)与圆![]() 相切的直线
相切的直线![]() :
: ![]() (其中
(其中![]() )交椭圆
)交椭圆![]() 于点
于点![]() ,
, ![]() ,若椭圆
,若椭圆![]() 上一点
上一点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市通过随机询问100名不同年级的学生是否能做到“扶跌倒老人”,得到如下列联表:
做不到 | 能做到 | |
高年级 | 45 | 10 |
低年级 | 30 | 15 |
则下列结论正确的是( )
附参照表:
| 0.10 | 0.025 | 0.01 |
| 2.706 | 5.024 | 6.635 |
参考公式:![]() ,其中
,其中![]()
A. 在犯错误的概率不超过![]() 的前提下,认为“学生能否做到‘扶跌倒老人’与年级高低有关”
的前提下,认为“学生能否做到‘扶跌倒老人’与年级高低有关”
B. 在犯错误的概率不超过![]() 的前提下,“学生能否做到‘扶跌倒老人’与年级高低无关”
的前提下,“学生能否做到‘扶跌倒老人’与年级高低无关”
C. 有![]() 以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低有关”
以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低有关”
D. 有![]() 以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低无关”
以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】旅行社为去广西桂林的某旅游团包飞机去旅游,其中旅行社的包机费为10000元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在20或20以下,飞机票每人收费800元;若旅游团的人数多于20,则实行优惠方案,每多1人,机票费每张减少10元,但旅游团的人数最多为75,则该旅行社可获得利润的最大值为( )
A. 12000元B. 15000元C. 12500元D. 20000元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() 分别是
分别是![]() 的中点将
的中点将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 重合于点
重合于点![]() .则下列结论正确的是( )
.则下列结论正确的是( )

A. ![]()
B. 平面![]()
C. 二面角![]() 的余弦值为
的余弦值为![]()
D. 点![]() 在平面
在平面![]() 上的投影是
上的投影是![]() 的外心
的外心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经国务院批复同意,郑州成功入围国家中心城市,某校学生团针对“郑州的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图1所示茎叶图.
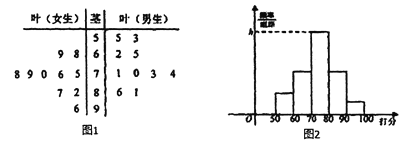
(1)分别计算男生女生打分的平均分,并用数学特征评价男女生打分的数据分布情况;
(2)如图2按照打分区间![]() 绘制的直方图中,求最高矩形的高;
绘制的直方图中,求最高矩形的高;
(3)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com