
平行四边形ABCD中, ·
· =0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,则三棱锥A-BCD的外接球的表面积为( )
=0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,则三棱锥A-BCD的外接球的表面积为( )
A.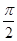 | B. | C.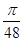 | D. |
科目:高中数学 来源: 题型:单选题
四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯,如图所示.盛满酒后他们约定:先各自饮杯中酒的一半.设剩余酒的高度从左到右依次为h1,h2,h3,h4,则它们的大小关系正确的是( )
| A.h2>h1>h4 | B.h1>h2>h3 | C.h3>h2>h4 | D.h2>h4>h1 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某几何体的三视图如图所示(俯视图是正方形,正视图和左视图是正三角形),根据图中标出的数据,可得这个几何体的表面积为( )
A. | B. | C. | D.12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com