
| A. | [$\frac{3}{4}$,1) | B. | [$\frac{1}{8}$,$\frac{\sqrt{3}}{6}$) | C. | [$\frac{3}{16}$,$\frac{1}{2}$) | D. | [$\frac{3}{8}$,3) |
分析 作出f(x)的图象,以及直线y=t,方程f(x)=t有两个不等的实根,即为直线y=t和y=f(x)的图象有两个交点,分别求得x1,x2的范围,由不等式的性质,即可得到所求范围.
解答 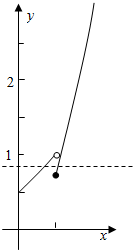 解:函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{2},x∈[0,\frac{1}{2})}\\{3{x}^{2},x∈[\frac{1}{2},1]}\end{array}\right.$,
解:函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{2},x∈[0,\frac{1}{2})}\\{3{x}^{2},x∈[\frac{1}{2},1]}\end{array}\right.$,
作出f(x)的图象,以及直线y=t,
方程f(x)=t有两个不等的实根,即为
直线y=t和y=f(x)的图象有两个交点,
由x+$\frac{1}{2}$=$\frac{3}{4}$,可得x=$\frac{1}{4}$,
由1=3x2,可得x=$\frac{\sqrt{3}}{3}$(负的舍去),
即有$\frac{1}{4}$≤x1<$\frac{1}{2}$,$\frac{1}{2}$≤x2≤$\frac{\sqrt{3}}{3}$,即$\frac{1}{4}$≤x22≤$\frac{1}{3}$,
则x1•f(x2)=3x1•x22∈[$\frac{3}{16}$,$\frac{1}{2}$).
故选C.
点评 本题考查函数和方程的转化思想,考查数形结合的思想方法,同时考查不等式的性质和运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
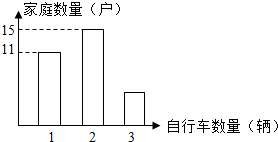 某个小区为了制订自行车棚的整修方案,进行了一次以家庭为单位的自行车数量调查.按照家庭成员的人数采用分层抽样的方法,一部分数据如表所示,其中m=2n.通过调查统计了每个家庭的自行车数量,将结果绘制成条形图,如图所示.
某个小区为了制订自行车棚的整修方案,进行了一次以家庭为单位的自行车数量调查.按照家庭成员的人数采用分层抽样的方法,一部分数据如表所示,其中m=2n.通过调查统计了每个家庭的自行车数量,将结果绘制成条形图,如图所示.| 家庭人数 | 1 | 2 | 3 | 4 | 5 |
| 家庭数量 | 6 | m | 72 | 18 | |
| 抽样数量 | 4 | n | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com