
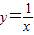 在(-∞,0)∪(0,+∞)上是减函数;
在(-∞,0)∪(0,+∞)上是减函数; ;
;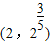 ,则当x>1时,该函数的图象始终在直线y=x的下方;
,则当x>1时,该函数的图象始终在直线y=x的下方;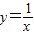 在(-∞,0)和(0,+∞)上分别是减函数,在(-∞,0)∪(0,+∞)上没有单调性;
在(-∞,0)和(0,+∞)上分别是减函数,在(-∞,0)∪(0,+∞)上没有单调性;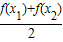 和f(
和f( )的大小;
)的大小;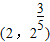 ,知f(x)=x
,知f(x)=x ,由此能求出结果;
,由此能求出结果;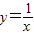 在(-∞,0)和(0,+∞)上分别是减函数,
在(-∞,0)和(0,+∞)上分别是减函数,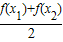 -f(
-f( )
) -[-(
-[-( )2+1]
)2+1] -
- <0,
<0, ,故②正确;
,故②正确;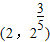 ,∴f(2)=
,∴f(2)=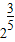 ,故f(x)=x
,故f(x)=x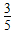 ,
,

 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
| 2x+2014 |
| 3x+7 |
| π |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| π |
| 6 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)如果一事件发生的机会只有十万分之一,那么它就不可能发生;
(2)如果一事件发生的机会达到99.5%,那么它就必然发生;
(3)如果一件事不是不可能发生的,那么它就必然发生;
(4)如果一件事不是必然发生的,那么它就不可能发生.
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 2x+2014 |
| 3x+7 |
| π |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| π |
| 6 |
| π |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com