
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)射线![]()
![]() 与曲线
与曲线![]() 交点为
交点为![]() 、
、![]() 两点,射线
两点,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,求
,求![]() 的最大值.
的最大值.
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)过椭圆的右焦点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 、
、![]() ,其中直线
,其中直线![]() 交椭圆于
交椭圆于![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于
于![]() 点,求证:直线
点,求证:直线![]() 平分线段
平分线段![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是边长为2的正方形,SA=SB=SC=SD![]() ,点E,M,N分别是BC,CD,SC的中点,点P是MN上的一点.
,点E,M,N分别是BC,CD,SC的中点,点P是MN上的一点.
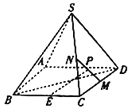
(1)证明:EP∥平面SBD;
(2)求四棱锥S﹣ABCD的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农贸公司按每担200元的价格收购某农产品,并按每100元纳税10元(又称征税率为10个百分点)进行纳税,计划可收购![]() 万担,政府为了鼓励收购公司多收购这种农产品,决定将征税降低
万担,政府为了鼓励收购公司多收购这种农产品,决定将征税降低![]() (
(![]() )个百分点,预测收购量可增加
)个百分点,预测收购量可增加![]() 个百分点.
个百分点.
(1)写出税收![]() (万元)与
(万元)与![]() 的函数关系式;
的函数关系式;
(2)要使此项税收在税率调整后不少于原计划税收的![]() ,试确定
,试确定![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次体育兴趣小组的聚会中,要安排6人的座位,使他们在如图所示的6个椅子中就坐,且相邻座位(如1与2,2与3)上的人要有共同的体育兴趣爱好.现已知这6人的体育兴趣爱好如下表所示,且小林坐在1号位置上,则4号位置上坐的是
小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |

A.小方B.小张C.小周D.小马
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在15-75岁之间的100人进行调查, 经统计“青少年”与“中老年”的人数之比为9:11
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“一带一路”是否和年龄段有关?
的把握认为关注“一带一路”是否和年龄段有关?
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查.在这9人中再选取3人进行面对面询问,记选取的3人中关注“一带一路”的人数为X,求X的分布列及数学期望.
附:参考公式 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com